第一章:王炸(理科宪法)
理科宪法第二条:化繁为简
高手有王炸。
理科的大小王,是理科的两条最高游戏规则。
其中的小王,也就是宪法第二条,是「化繁为简」。

科学家丁文江说:
科学是教育和修养最好的工具,学科学的人有求真理的能力,而且有爱真理的诚心。无论遇见甚么事,都能平心静气去分析研究,从复杂中求简单,从紊乱中求秩序;了然于宇宙生物心理种种的关系,才能够真知道生活的乐趣。
「从复杂中求简单,从紊乱中求秩序」,这是指导我们理科学习研究实践的核心原则。
理科顶尖的玩家,这一条都是内化到思维当中,形成本能。
小王牌的守护神,是牛顿。
他是「从复杂中求简单,从紊乱中求秩序」的顶级玩家。
当时他研究天文,想要找到天体运作规律。一个难题是望远镜质量不过关。这个质量既有工艺的因素,也有理论的因素。
牛顿自己研究了光学理论,提出了反射式望远镜的构想,发明了第一架反射式望远镜,从而大幅度改进了观察天体的质量。
新望远镜的研发过程,本身就是一个难题。牛顿在经过多次研制非球面的透镜都不成功后,才决定用球面反射镜作为望远镜主镜。
牛顿为了更好的研究,自己动手造观测工具。而为了造出高水平的工具,又要搞定光学的原理以及相关的各种问题。
而后面,为了分析物理运作规律又发明了微积分。
总之遇到困难就深入研究逢山开路遇水搭桥,一路破除重重迷雾,你以为他只是发现了牛顿三定律啊?他是为了吃火锅自己还发明了锅和电磁炉。
而他所做的一切,其实都是围绕「从复杂中求简单,从紊乱中求秩序」。
那么你呢?
你在遵循宪法第二条吗?
还是在「持续违宪」?
为什么学了奥数还是思维不行
在应试教育中,老师教育大家「要什么题型都见过、要做熟练,这样将来考试才会做」。
所以这种方法,自然就要大量刷题。你必须见过了,熟练了,才行。
但是顶级的高手,往往不刷题型。
直接用思维去解决难题,哪怕没见过,也没关系。
一次搞定。
这样自然就省事了。
有年暑假我回老家,跟亲戚一块吃饭。
我外甥在读小学五年级,周末还要上奥数班。
去饭店的车上,我问他奥数班都在教什么呀,他说教了鸡兔同笼。
我问那么到底老师怎么教的呢。
老师教了他们,这种题目要用假设法。先假设都是鸡或者兔子,看有多少腿。然后再比较差异。
那么为什么要用假设法呢?
小朋友说:「这个老师就没教了」。
作为一个从小热爱学习但反感应试教育的人,我人生最喜欢吐槽的就是愚蠢的教育体系。
学生菜菜一个,老师菜菜一班。
应试老师就会灌输知识和套路。
例如这个奥数班,老师教了大家「假设法」这个知识点,要大家记住可以用它来解决鸡兔同笼类问题,知识套路灌输到位。
接下来嘛,那就是给题目让同学们刷了,形成条件反射。这样将来「看到鸡兔同笼类问题」就知道用「假设法」。
这就是「把题型套路刷熟练,从而能够解题」。
然而高手,可以直接运用「化繁为简」思维搞定,无需先看解法、无需刷题。
在小王的指导下攻克难题
例如我们看到题目:
鸡兔同笼,共38个头,112只脚,那么鸡有多少只?兔有多少只?
用「从复杂中求简单」的思路:
这题目我们没见过没做过,怎么思考呢?
好像做不出来呀,太复杂了。
我们能不能【简化】呢?从题目中【简化】出我们能做的,然后看看如何逼近到最终的问题?
那么,这道题的【复杂性】在哪里呢?
因为又有鸡又有兔子,很难计算,无从下手。
要是【简化】的话,就应该是只有一种动物,这样简单很多。
那么我们假设笼子里只有鸡,一共38个头的话,就应该有38只鸡。
每只鸡两只脚,那就是76只脚。
然而题目里一共是112只脚。差了36只。
这个差异怎么来的呢?有些兔子被我们假设成鸡了。
那么到底有多少兔子呢?
这个比较复杂,难以想清楚,我们就一步一步来嘛。
目前我们假设所有都是鸡,没有兔子。
那么我们走出一小步,如果有一只兔子呢?
这时候应该是37 x 2 + 1 x 4 = 78只脚。
或者,因为少了一个兔子多了一只鸡,而兔子比鸡要多了两只脚,所以应该是76 + 2 = 78只。
如果有两只兔子呢?那就应该是 78 + 2 = 80只。
这样我们也就能找到规律了。
每用一个兔子换掉一只鸡,就会多出两个脚。
而目前我们差异是36只脚,36 / 2 = 18。
应该有18只兔子,而鸡是 38 - 18 = 20只。
验算一下: 2 x 20 + 4 x 18 = 40 + 72 = 112只。
正确。
基于简化思维,我们自己从头把鸡兔同笼化简,通过研究思考,得出了答案,还自己研究产生了「假设法」这个知识点。
基础智力训练了,新知识获得了,题目会做了,还不用反复刷。
完美!
理科宪法第一条:爱智求真
第二条「化繁为简」是实践论,而第一条「爱智求真」则是价值观。
价值观指导实践论。

在我们的扑克中,「爱智求真」的守护神,是泰勒斯。
为什么牛顿在小王牌上,他在大王牌上?
难道他比牛顿还牛?
某个意义上,的确是。
因为泰勒斯是首创理科的人。他是祖师爷,奠定了理科的核心规则。
而牛顿,可以说是再创理科的人。
打个不恰当的比方。
泰勒斯是刘邦,开创了汉朝。
牛顿是刘秀,再造了汉朝。
所以我们理科学习,应该拜这两位祖师爷。
那么为什么要爱智求真呢?
为了成为自由的人。
这个观念,是古希腊哲学家提出来的。
泰勒斯,就是第一位希腊哲学家,开天辟地之人。
希腊哲学是现代理科,包括数学、物理等的源头。
那么到底什么是哲学呢?它和今天的数学物理有怎样的关系呢?
成为自由的人需要有理性和智慧
希腊哲学家认为,学习和思考的目的,旨在成为自由的人。
那什么是自由的人呢?
古代的希腊,沿海一带,发展出了商业社会,海洋文明。跟其他地区,有很多海上贸易来往。
要展开贸易,就需要有契约。而契约有效的前提,是立约人是独立自主的,有权立约。也愿意承担相关的责任,并能力承担责任。
这样的人,也就是「自由人」。他有权力决定自己的行动,要为自己的行为负责,也有相关的能力来承担责任。
自由是权力、责任与能力的平衡。而不是「想干什么就干什么」。
就像开车上路,首先要学驾驶,获得驾照(确保有能力开车,能承担对自己和他人的安全责任),要强制买保险(确保出事了能承担责任)。有了这些,才有开车上路的权力。脱离责任、能力谈权力,往往是灾难。
在希腊罗马社会中,跟「自由人」对应的,是「奴隶」的概念。
罗马人对「奴隶」的解释是「无法自主掌控自己命运的人」。奴隶没有对国家的权力(例如无法投票选举官员),也没有对国家的责任(无需纳税)。
反之,公民(自由人)对国家有权力,同样对国家有责任,例如交税、服兵役。凯撒鼓舞他的士兵说:「诸君是罗马公民」。意思是,你们对国家是有责任的。
从这个角度,传统学校教育中,很多学生在学习上都是奴隶,因为缺乏权力和能力,不能承担全局的责任,无法自主掌控学习,只能被动的依赖外部资源。
你希望自己或者孩子,成为学习上的奴隶,还是可以自主学习的自由人?
意志自由与理性自由
人如何能得到自由呢?
这里就出现了两个概念:意志自由与理性自由。
所谓意志自由,就是按照自己的想法行事,想干什么就干什么。
然而这种自由,有一个问题,就是表面上看上去的「想干什么就干什么」,背后常常却是不自主的。
例如十年前,上海满大街都是LV的包包。女人为什么都要买LV包包呢?很多人是因为觉得自己不买就没面子等。
那么,到底她们买包,是「自由选择」,还是不自由的呢?
回到本文的「韭菜」话题,股市里各种韭菜,他们进入股市、买进卖出,都是自己的操作,他们是「自由」的吗?有多少人是受到市场情绪、虚假信息、低级判断的操控?
希腊哲学家认为,要想自由,就需要把握真相、看透事物背后的规律,从而能够做出高质量的判断。
这种自由叫做「理性自由」。
真相让你自由。
在《庄子·养生主》中,有庖丁解牛的故事。说庖丁杀牛十九年,一把刀依然锋利,像新的一样。为什么呢?庖丁说「以无厚入有间,恢恢乎其于游刃必有余地矣」,也就是把握了牛的结构脉络规律,于是「游刃有余」。
从这个意义上,学神是掌握了学习的真相从而获得了学习自由(游刃有余)的人,股神是掌握了股市的真相从而获得了投资自由(游刃有余)的人。
希腊人推崇「理性自由」。他们认为,要了解真相,就需要有智慧。爱自由追求自由,就需要爱智慧追求智慧。
爱智慧,学数学
希腊哲学是现代科学和人文思想的重要源头。而哲学的英文philosophia,由两个部分组成:philo的意思是爱,sophia的意思是智慧,哲学的本义,是爱智慧、追求智慧、追求真理。
注意在希腊人的观念中,他们认为「智慧」是神的能力,所以一个人只能追求智慧,而不能最终达到智慧的境界。「爱智者」,是追求智慧的人。
而我们中国人的观念中,更习惯讲「智者」,智者是拥有智慧的人。当然这也是源于对智慧的追求。
那么如何追求智慧、提升智慧呢?
希腊人把数学当作基本的教育手段。
这当中一个重要的人物,是柏拉图。

柏拉图在他四十多岁的时候,回到雅典,创建了自己的学校:柏拉图学园。这是西方文明最早的有完整组织的高等学府之一,也是中世纪西方大学的前身。
为了追求智慧,柏拉图在学园中关注4个科目:算术(arithmetic)、几何、音乐、天文。
注意,在这里arithmetic的翻译,也是算术。当时译者采用了我们已经存在的「算术」词汇。
这里面就形成了一个容易混淆的地方。
古希腊人说的arithmetic,其实更偏向于今天的数论。研究数的性质、关系,例如质数和合数,而非单纯的计算。它是一门更看重研究、逻辑推理的学科,而非关注计算技能的学科。
在柏拉图以及很多希腊精英眼里,计算这种技能,更多的是小贩之类手工业者、以及奴隶要掌握的。精英需要思考。
而「算术」这个词,如前所述,在中文的含义中,偏向于计算技术/技能。
这两者,差别很大。
柏拉图是怎么看待这四门科目的呢?
援引WikiPedia上的内容:
音乐教育比其它教育重要的多,它可以陶冶心灵,使性情得到调和,其原因是节奏和乐调有强烈的力量浸入心灵的最深处。算术不仅能训练人的计数能力,而且还能提高人的抽象思维能力和判断能力。
学习几何是因为军事上安寨扎营、测量作战阵地和编队布阵需要初步的几何学知识。学习天文能设想和把握人的肉眼不能追逐的天体运作,从整个宇宙中发现和谐的美和完善。所以,他认为算术、几何和天文的真正价值在于唤起人对宇宙奥秘的思考,发展和完善人的思考能力。于是,柏拉图将算术、几何、天文和音乐理论四门课程列入教学科目,并在教学活动中广泛传授。
这四门科目,柏拉图称为「liberal arts」,自由之艺。
柏拉图的「自由之艺」,开创了西方大学的思想基础。
直到今天,美国有很多文理学院(Liberal Arts College),是美国高等教育的重要种类之一。
摘录百度百科的解释:
这种文理学院,通常以本科教育为主,规模小而精。在教育思维上,注重全面综合教育,强调发掘学生的思维潜能,实现真正意义上的全人发展, 其课程设置以基础学科为主,涵盖艺术、人文、自然科学、社会科学等门类, 以此来区别于以职业培训或科学研究为导向的综合性大学及各种专业学校、技术高校。
理念上听起来很好,然而这种文理学院,整体也是落后于整个时代了。
而「liberal arts」这个词,在中文被翻译为「博雅教育」。对这个翻译,我的感觉很复杂。一方面觉得非常的优雅,某种程度上也非常切题。
但另一方面,「博雅」这个翻译,似乎跟「自由」又有很大的差异,容易让不理解本源的人造成误解。就跟算术的翻译一样。
大体而言,博雅是形式,而自由是实质。
各位如果在考虑留学,一定要警惕网上的各种宣传,比如「博雅教育理念」啊吧啦吧啦。如果听上去觉得对某些学校产生了非常高大上的感觉,当心。很多留学中介是吹牛不打草稿的。
在柏拉图学园的门口,写着「不学几何者,不得入内」。
这不是让你去考试刷分的,是让你去追求智慧。
柏拉图第一次确立了几何作为学校四门主科的地位,所以在我们的理科思维扑克中,他担当了红桃7(几何图形)的守护神。
在学几何之前,你可以拜一下柏校长。

自然哲学与人的哲学
严格的说,其实他们当时并没有「数学」这个概念,他们在研究哲学。
哲学又可以概略分为两类:
- 自然哲学
- 人的哲学
自然哲学,重点就是研究自然原理,数学、物理、化学、生物等等,都在这个范畴之类。
数理化的清晰分科,是近代科学革命后的事情。在古代,这些都在「自然哲学」里。
也就是说,「自然哲学」其实就是古代的理科。
一直到牛顿发现三大定律,他的著作名称,都叫做「自然哲学的数学原理」。牛顿可以说是最后一位自然哲学家,因为他之后,就开启了分科的时代。
理科理科,探索事物原理的学科。
而理性心智,以爱智求真、溯本求源驱动,本身就是理科的思想基础。反过来我们通过理科学习,不仅仅是是探索了解世界的真相,也是发展我们的理性心智。
理科自身的立足点就是「求真理求真相」,老师却告诉大家死记硬背知识点,只要会刷题能得分就可以。
这不光是方向反了。
这是离经叛道背叛师门了。
理科祖师爷泰勒斯
希腊历史上的第一位哲学家,也是第一位自然哲学家,是泰勒斯。

泰勒斯生平大致在公元前620年到公元前545年。
在那个时代,大多数人都以神话或者传统教条理解自然现象(迷信),其实到今天很多人依然高度迷信。
泰勒斯是希腊历史记载的第一个用观察和逻辑解释自然现象的人。
我们前面谈到,自然哲学其实是古代的理科,泰勒斯是开创理科的祖师爷,是那个身体力行设定理科宪法的人。
人类的先知。
泰勒斯认为我们经验观察产生的结论未必可靠。
如果要寻求真相,那就需要严谨求证。
他是第一位提出观念需要证明的思想家。
那么如何求证呢?他首创了「数学证明」的思想和方法,成为第一个做出数学证明的人,开创了数学证明的传统。
这个思想,到今天还是超前大多数人。
顶级大佬有一个特征,就是他们的思想,跨越千年,依然是本质和领先,实现了不朽。
就像孙子兵法,作为战略学开山之作,到今天依然是顶尖思想。在美国亚马逊排行榜上(注意是英文不是中文),在哲学类排名第一。
顺便说一下,在理科思维扑克中,孙子在黑桃A上,策略之神。

泰勒斯的一个案例,是对「对顶角相等」的证明。
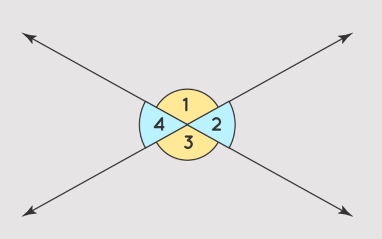
1)观察:两线相交,对顶角看起来相等
2)质疑:是否总是相等?为什么相等?
3)证明
已知相邻角互补(=180°)
∠1 + ∠2 = 180°
∠1 +∠4 = 180°
所以 ∠2 = ∠4
这个相对简单,但是要注意是这个范式,我们观察产生的经验结论,要经过证明确认其真实性。
这个思想,对于认知水平至关重要。
基于质疑精神,我们可以继续对这个证明提出质疑。
证明中引用了「已知相邻角互补」作为前提,那么为什么「相邻角互补」呢?请证明之。
这样一层一层下去,难道没有尽头吗?
是否会追溯到最基本的无需证明的观点/事实呢?
这就引出了第一性原理(梅花2)。

学渣用经验解释经验,学神形成严谨抽象概念
泰勒斯有一个观念,就是要从直观经验中提炼规律。
很多时候,这种提炼就会形成抽象概念。
例如,他观察月亮、盘子、车轮等事物,这种人们称为「圆」。
从月亮、盘子、轮子这种事物,我们提炼出「圆」这个抽象概念,其实就是在总结规律。
这个是比较好总结的。
那么什么是圆呢?你能给他下一个定义吗?
大多数人(无论是古人还是今人)往往会说:「像月亮、盘子、轮子这样的东西,就是圆」。
这还是用现象来解释概念,而非找到这些事物的本质特征。
甚至还有人会说:「像月亮、盘子、轮子这样的圆圆东西,就是圆」。
让你来定义什么是「圆」,圆都还没定义,你就用「圆圆」这个没有定义过的来定义圆自己,矛盾了。
大多数人其实连这种矛盾都看不出来。
反过来,认知水平高的人,对概念就敏感,善于提炼、识别、分析。
泰勒斯当时给圆下的定义是:
和某一点距离相等的点组成的轨迹,就是圆
大家注意了,这就脱离了举例法的定义,而是描述了圆的抽象本质规律了。
这样描述的圆,就是理论上的纯粹的抽象,超越了现实例子的不完美,例如车轮很难真正做到这么圆。
这个定义从经验世界出发,定义的圆,脱离了经验世界的具体对象,完成了抽象过程,提炼了本质规律(到定点的距离等于定长)。
今天初中数学中圆的定义,就是基于泰勒斯提出的范式。
基于这个定义,进一步细化,「某一点」我们称为「圆心」,「距离」我们称为「半径」,这样新的概念就出来的。
高中基于集合论,把它做了一个变化,定义类似于:
到定点的距离等于定长的点的集合。
但发现本质规律、实现抽象定义的,还是泰勒斯。
理科学神普遍的特征,就是像泰勒斯这样,日常会观察研究分析思考,尝试去从现象中提取规律形成概念。
他们往往会自己去定义概念。
哪怕是书上的概念,他们也会自己去思考概念怎么来的,完成研究推导分析提炼的过程。
然而大多数同学,就是死记硬背,把书上的概念抄几遍背下来。
老师就是这么教的。
这背后的问题,是老师普遍也理性心智欠缺,大多数老师以前也是靠死记硬背刷题考大学的,而不是靠研究分析理解形成底层智慧。
低认知水平培养低认知水平。
认知水平低下的人,本能的觉得概念不重要。然而高认知的人,对基础概念无比重视。
学渣关注How,学神关注Why
了解事物有三个基本维度,我称之为WWH模型:
- Why:为什么
- What:是什么
- How:怎么做/怎么用
对于WWH核心关注点的差异,反应了学习者的层次:
- 学神(最关心的是Why)
- 学霸(会关注到What)
- 学渣(只关注How)
大多数同学包括老师,最关注的就是How,怎么解题。
这种水平都很渣。
低层次的家长、老师和同学,往往how搞不定,去咨询什么的,又抱着一种观念「不要跟我讲什么原理、概念,告诉我怎么做」。
这种想法非常愚昧。
理科之所以叫做理科,意思就是「探索原理的学科」,原理是Why和What。
你只管How学什么理科啊。
顶尖的同学,往往是深度探索底层原理Why的,进而把概念的What搞清楚,而原理搞懂了,概念扎实,解题的How其实简单很多。
用泰勒斯研究提炼圆的概念的例子。
我们看到车轮、盘子、月亮的相似性,可能会提炼出一个概念例如圆,就完了。
这个比较容易,因为看上去就像。
但是泰勒斯会研究思考,到底为什么(Why)它们看上去很像呢?它们的共性是什么呢(What)。
研究分析发现,原来它们共同的规律是,它们的那一圈边缘,到某个点的长度相等。
把为什么搞清楚了,圆的定义也就呼之欲出了。未来可以运用这个知识点。
Why -> What -> How。
通过搞清楚来源去提炼产生概念知识。
哪怕我们学习,课本上已有的知识,要学透,也要经过这个逻辑,重新分析推导。
大多数同学并不是这样的,他们直接背定义。
顶尖学神会怎么学习呢?
课本上看到了定义(What),也会反过来研究思考为什么(Why)会产生这个概念。
很多时候课本上是有相关内容的,只是大多数同学忽略了。哪怕没有,顶尖学生也会自己思考尝试建立推导逻辑。
例如你先看到了圆的定义,反过来思考这个推导出来的。
我们看月亮、看盘子,能看出来到定点的距离等于定长的规律吗?
好像直接看比较困难。
看车轮呢?
我靠,车轮好像比较容易,因为很多车轮是有辐条的,辐条都连接到一个中心上。
而这些辐条好像都有一个规律,长度差不多啊。
你从这个角度思考,理科祖师爷泰勒斯,可能是从车轮来发现这个规律的吧,相对简单。
当然这只能是猜想了。
提升难度,如何从月亮、盘子这种东西,来发现识别这个规律呢?
车轮辐条跟他们相比,貌似加了一系列辅助线,从而让规律更容易浮现出来。
那么到底如何加辅助线,这个逻辑是什么?
让我们观察月亮、盘子这种东西,至少有一种特征比较明确,那就是貌似它们有对称性。
对称性是「线索武器♦️」中非常重要的一张牌,方块K。

让我们想象折叠,会产生对称轴。
这样的对称轴有多少根呢?好像会很多。
那这些对称轴之间有什么关系呢?
我们尝试再折叠一次,或者画对称轴。发现它们会有一个交点。
再来,好像还是会相交在一点。
这一个点非常特殊了。
很有意思。
它特殊在那里呢?
比较容易发现,它和边缘上的点貌似距离相等。
这也出来结论了。
于是这样,我们利用「对称性」、「折叠」,自己干出辅助线来发现了规律。
重新走完了研究定义「圆的概念」路程,自己提炼创造了这个概念。
就是费曼所说:
凡我不能创造的,我就没有理解。
你把基础概念重新创造了,就理解了。
这才是学神的学习方式。
无需记忆,只需理解。
为了理解,研究创造。
菜鸟回答别人出的题,高手提出自己的问题
另外需要注意一点,大多数同学,是做老师出的题目。
而前面,我们研究圆的概念时,其实是反过来,从这个定义结论出发,反向出题:
如何从盘子、车轮、月亮这些日常现象中,提炼出圆的定义?
通过这个反向的问题,从What去寻找Why,从而实现真正深刻的理解。
这其实运用了基于逆向思维的倒推法(黑桃2):

而且通过这个自创问题,我们还研究出两种解法。
一种从车轮入手,简单(因为自带辐条甚至辐心的辅助线)。
一种从更抽象的只有边缘没有辅助线的月亮、盘子等研究思考,利用「对称性」等入手探索。
这道题目自己研究思考下来,那对思维的训练很不错了。
第二种情况还是有难度的。
你这样走一遍,不仅仅是深入创造理解了概念,还做了一题多解,有了对对称性、辅助线利用的新思路。
头脑就是这样灵活起来的,逻辑就是这样强大起来的。
解题经验丰富了,概念透彻了。
完全是在研究课本阶段就能变得很厉害。
这里就有一个结论:
吃透课本知识的What-Why-How,不用额外的习题,就已经可以成为一流水平。
当然你还是要刷一些题巩固提升,但整体水平直接在吃透课本层面搞定了。
这时候就非常省事。
知识扎实、解题经验丰富,大多数题目一看就知道怎么回事跟哪些知识有关系。少数难以解决的,也可以研究分析。
我在中学时代就发现一件事情,就是绝大多数题目,我看一眼就知道考察什么知识点,直接干出来就完了。核心在于研究理解搞清楚了基础概念。
我的同学就不行,他们需要用那种「题型资料」,靠题型反过来刷熟练度,看到题型要形成条件反射,才知道哪种情况用什么知识点。
但是题型教辅里面又是一啪啦新的内容和知识啊,题型本身也是知识。
我只需要学课本,他们还要学题型教辅刷题,我根本就没有后面这块工作量。
这里面有个荒谬之处,就是我的学习能力更强,但我只需要学好课本;他们学习能力不足,课本学不好,但课堂内容还得学,同时还有增加要「熟悉各种题型能应用自如」的任务,工作量还比我大很多。
他们更没这个能力呀,又回到能力圈的问题了。
你连课本基本概念知识都没搞清楚,还去搞题型,这些题型五花八门,你有那个精力和本事吗。
关键是还不止数学一科,其他的还要花费时间呢。
为了解决一个问题,制造出更大的问题。
但他们认为是对「基础知识不牢」的解决方案。
这又是认知水平不同导致的差异。
砍掉学习任务量,一个核心就是砍掉你去套题型的任务量。不管千变万化,回归基础概念和思维,用吃透课本解决95%的问题。
归根到底,你先要对「基础概念知识体系」有深刻的认知,这才是应对千变万化题目的基础。
以不变应万变。
简单愉悦省事。
一切法律与宪法抵触者,无效
在法律体系中,宪法处于最高地位。
一切法律与宪法抵触者,无效。
我们看「法律」这个词的英文,和「规律」本来也就是一个词,LAW。
在理科学习中,同样的道理。
学习行为和「理科宪法」违背者,无效。
回归我们的两条宪法:
1)大王:爱智求真

2)小王:化繁为简

以泰勒斯和牛顿为代表的理科大佬,正是发现、制定和有效执行宪法的人。
今天同学们看上去努力,然而行为普遍违宪。
大家关心的成绩和分数,而不是修炼智慧探索真相。
大家普遍把简单问题搞复杂,很少去思考复杂性在哪里,如何有效简化。
你可能很努力。
然而你是个理科法盲。
天天违宪而不自知。
所以被惩罚、被这些大佬发现发明的知识虐得死去活来,也就不足为奇了。
反之,真正理解了理科宪法的同学,往往是爱得死去活来,觉得学习和解题充满了乐趣。
4种花色、4大能力
虽然宪法有最高地位,但是没有其它法律来落实,那也是空的。
在理科思维扑克中的4种花色,就是用来落实宪法的。
它们代表了4种武器、4种能力:
- 红桃♥️ (现象武器): 表达能力
- 方块♦️ (线索武器): 观察能力
- 黑桃♠️ (策略武器): 谋略能力
- 梅花♣️ (规律武器): 哲思能力
每个花色13张牌,总计52张,就构成了捍卫宪法的核武库。
真理,需要由武器来捍卫。