第二章:红桃(现象武器)
红桃:现象武器与表达能力
在理科思维扑克中,红桃花色代表现象武器,对应着表达能力。
如果说语文看重表达能力,大家会本能赞同;然而数学看重表达能力,可能觉得一头雾水,觉得这东西最多算是个很次要的辅助技能。
然而真相恰恰相反。
归根到底,理科的研究流程,是「从现象到真相」的过程。
那么首先就涉及到,如何描述表达现象。
很多时候,我们之所以「看不清真相」,首先就是因为「现象的不清楚」。
有一年春节亲戚聚会,我外甥当时上小学二年级,他背着书包来到了餐厅,拿出了作业本。一问就是在学奥数,他妈(我表妹)给他报了奥数班,还有作业没完成。
有道题他不会,于是我表妹给他讲了一遍。讲的内容是应该怎么解(第一步干嘛第二步干嘛)。
然后外甥还是一脸懵逼。
他妈的语气开始不耐烦、更不耐烦,脸拉长,要爆了......
重复讲了两遍之后,她问:「你懂了没有」。
小朋友摇摇头,看见妈的脸色更凶了,又点点头。
她终于爆了,开始找老公:「你过来,来教一下你儿,气死我了,这么简单讲了几遍他都不会」。
我看了一下题目,大概是这样的:
小明家的鱼塘里养了草鱼、鲤鱼、鲢鱼和黑鱼,已知草鱼和鲤鱼一样多,黑鱼比草鱼少2条,鲢鱼比黑鱼多1条,鲤鱼有5条,问鱼塘里一共有多少条鱼?
我一看就觉得这题目根本不该在二年级引入。太复杂条件要素太多,二年级小朋友难以理解。
要我就根本不会让小朋友做这道题甚至上这个所谓的奥数班。
话分两头,亲妈败阵后亲爹上场。他很和蔼的又把解题过程讲了一遍。
我们先算草鱼,草鱼=5。
再把黑鱼求出来,5-2=3。
再求鲢鱼,3+1=4。
最后把它们加起来:5 + 5 + 3 + 4= 17。
很简单啥
懂了吗?
小朋友继续做懵逼状。
她妈在旁边大声说:「我就是这样跟他讲的。要这么讲还需要你吗?平时学习你也不管,你聪明你上啥。」
很尴尬。
这时候小朋友外公听到了,拍马过来上场缓和局势了。说:「我来看看」。
他又给小朋友讲了一遍。
最后开饭了这题还是没搞定。
我靠我要不行了,笑死了。
一道题,从儿子、爸爸、妈妈到外公,一家四口上阵,为啥还是没能搞定呢?
爸爸、妈妈和外公三人上场,他们的动作都是一样的:讲一遍解题过程。
灌输方法。
但是小朋友是不懂方法吗?
不是,根本没到那一步,他连现象都没搞清楚。
对二年级小朋友而言,这鱼那鱼啥的,太复杂了,晕了。
如果有一个「清晰的表达」,那就容易看清楚。
打出我们的红桃6,画线段图来表达这些鱼的数量。
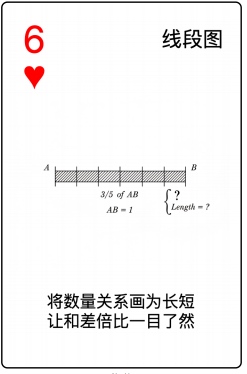
从「鲤鱼有5条」开始(因为只有这个是已知的)。
一下子就懂了。
这就是「清晰表达的力量」。
其实我们在现实工作中也是,例如同样去拜访一个客户,有些人写个拜访日志,能够把拜访过程、客户需求等写得很清晰,一看就明白,领导也马上明白需要给什么资源支持;有些人写出来混乱不堪,看到就头大简直像受刑。
这也是表达能力。
当然,如果是家长辅导小朋友画图,那是家长厉害。
而如果自己掌握了「清晰表达的武器」,那就是你自己厉害了。
红桃A:现象的两种表达
红桃A是提领整个红桃的核心牌:「现象的两种表达」。

整体来说,我们对现象的表达分为两类:
- 形象化表达
- 抽象化表达
形象化表达,旨在更贴近现实经验、人的感官和感觉。例如有画面感(针对视觉)、生动性(让人有体验感)。
而抽象化表达,旨在抽离表面元素,更贴近纯粹的底层逻辑、结构、原理,更贴近人的理性头脑。
这两者往往是相辅相成的,例如线段图,一方面是在形象化建立视觉体验,一方面其实也是在抽象提炼题目中的元素关系。
出色的表达能力,意味着需要对这两种表达有敏锐的觉察和丰富的手段。
红桃A的守护神,是达芬奇。
他是把形象表达和抽象表达融为一体,科技和人文合二为一的经典案例。
哪怕是画画这种形象化手段,背后依然是抽象化的逻辑。例如透视怎么弄,结构是什么如何表达。
就像参加素描班,看上去一个苹果很简单,画起来根本就不那么回事。
顺便说从绘画的角度,「写实」和「写意」两派,也就是「贴近形象表达」还是「贴近抽象表达」。
成为顶尖高手,要两手抓。
红桃中其它的牌,就是中小学数学中最常用、关键的表达武器,旨在「清晰的表达现象」。
13张牌如下:
- A: 现象的两种表达
- K: 函数
- Q: 方程与不等式
- J: 符号表示
- 10: 集合
- 9: 十进制表示法
- 8: 坐标系
- 7: 几何图形
- 6: 线段图
- 5: 数轴
- 4: 表格
- 3: 结构图
- 2: 示意图
这些牌的排序,大致是除了A,按照抽象表达到形象表达。
- K-9:抽象表达
- 8-2:形象表达
注意我前面谈到了,形象表达和抽象表达往往可能是融合的,所以可能一些牌既形象又抽象,这里只是按照主要特征大致分类。
从小学到高中的数学表达脉络
红桃中的大部份「表示武器」牌,是从小学到高中至关重要的核心知识。
而且它们之间,是有密切关系的。
同学们数学学习吃力,跟不了解这些「表达类知识」和它们背后的思维逻辑,有很大关系。
上次有位家长说,她女儿高二了,对于函数一直是稀里糊涂,虽然努力但是概念都不清楚。
这些不搞清楚,你数学就废了,刷题再多也没用。
首先它们是数学知识体系中的关键内容,所以你的数学体系会崩塌建不起高楼。
然后它们是解题至关重要的武器,所以你解题水平也会弱鸡(当然知识体系不行也是导致弱的重要原因)。
所以要搞清楚3个问题:
1)对为什么会有这些表达武器?
2)如何使用这些武器?
3)它们之间有什么关系?
符号表示:抽象表达的基石
在抽象表达牌中,最基础的一张是黑桃J(符号表示)。

黑桃J的守护神,是莱布尼茨。
为什么选择莱布尼茨作为「符号表示」的代言人呢?
因为他深刻的意识到了符号的重要性,在符号领域做出了深度研究,并且对整个世界产生了重大影响。
在代数符号方面,我们知道莱布尼茨和牛顿都发明了微积分,但是对于后世影响更大的,是莱布尼茨的微积分系统。一个重要原因就是,他的微积分的符号表示更清晰,牛顿的模糊很多。
这种影响力的差异,体现在哪里呢?我们来看一个简单的例子:求一个函数 y = x² 的导数(也就是变化率)。
牛顿的符号:他会在变量上方打一个点来表示其变化率。所以,他会写成 ẏ = 2x。
莱布尼茨的符号:他用 dy/dx 来表示 y 相对于 x 的变化率。所以,他会写成 dy/dx = 2x。
一开始,你可能会觉得牛顿的写法更简洁。但它的问题是「信息量太少」。那个「点」只告诉你「y在变化」,却没有告诉你「y是相对于谁在变化」。
而莱布尼茨的 dy/dx 符号,则是一个天才的设计。它不仅告诉你「y在变化」,还明确地指出了「y是相对于x在变化」。这个「d」就像一个操作指令,你可以对任何变量进行这个操作。更神奇的是,dy/dx 看起来就像一个分数,它在很多运算中,真的可以像分数一样进行「约分」和「拆分」(比如链式法则),这极大地简化了复杂运算的思考过程。
简单来说,牛顿的符号是一个「静态的标签」,而莱布尼茨的符号是一个「动态的、充满信息的操作符」。 正是这种清晰度和延展性上的巨大优势,让莱布尼茨的符号系统最终赢得了世界。
而在数字符号方面,他研究了二进制,而二进制后来成为计算机内部使用的数字系统。如果说农业时代运行在十进制之上,那么信息时代和AI时代运行在二进制之上。
顺便说一下,莱布尼茨对二进制的思考,源于易经的启迪。
易经是人类历史上辩证思维的先驱,传说是周文王所作。
辩证思维这张牌,是梅花Q。
 数学思维背后是哲学思维。
数学思维背后是哲学思维。
理科的精进,需要的不是天天刷茴香豆的4种写法,而是融会贯通人类文明的精华。
莱布尼茨清晰的认识到,创造和选择正确的符号,可以启迪我们更深刻的思考,发现真相。
我们学习理科,也要对此有清晰的觉察。
要有符号思维。
回过头看算术和代数领域,从「符号思想」出发,分别有两个最重要的符号表示:
1)算术领域:十进制表示法(数字符号)
2)代数领域:用字母表示数和量(字母符号)
从小学到高中,我们的数学都是建立在这两种表示法之上。
数字的符号表示:简化的需求
我们最早学习数学,是从认识0-9开始的。
0-9就是数字符号。
而且这种符号,是更加抽象的符号。
在它之前,往往还有相对比较形象的符号。
例如画几个点就表示几,或者画几根线就表示几。
但是这样不方便,如果你的数字越大,你画点画线的时间就越长。
越来越复杂。
基于简化原则,用抽象符号,例如0-9,这个你表示没有和表示九,画的笔画也差不到哪里去。
但光是符号化还不行,还是会面临复杂性问题。
这就引出了十进制。
为什么十进制总是教不会学不会
在理科思维扑克中,十进制是红桃9。

我们在小学入门阶段,十进制表示法是超级难点。
整体来说理解0-9比较容易,因为有手指头这个我们自带的形象化工具对应。但是10,等等,为什么10根指头成了这个样子了?
小朋友们会普遍懵逼,例如「11」,为什么两个1意义不一样?
那个乱啊。
事实上,家长和老师也会想办法帮助小朋友理解,还形象联系实际,但娃还是糊涂。
这里关键问题在于,按照课本和上面的教法,十进位这个知识点,看上去就像是从天上掉来的。没有为什么,就得学会。它不是一个自然生长长出来的知识点。
而十进制理解不透彻,后续各种知识都会有问题,例如加减法尤其是涉及到进位情况。
很多时候你看小朋友算加减法,一会对一会错。通常要么就是十进制没搞懂,要么就是后来的四则运算不明白。
刷很多题也没用,不明白就是不明白。
可以说小学前三年数学,踩的很多坑,都跟不理解十进位有直接关系。
数字符号表示的卡点:一一对应创造符号太复杂
让我们思考啊,从零到九,我们用了十个数字表示(0-9)。
那么接下来呢?难道每增大一个数目,我们就要为它创造一个新的符号?这样下去什么时候才是头啊?
甚至你可以引导小朋友尝试走一下这个路线,看看大家能创造多少个符号出来。
但显然,这种方式是不可持续的。越到后来符号越多也就越复杂。
你记符号都记不过来。
换句话说:「为每一个数字创造一个符号」的方式因为复杂性,不可持续。我们需要找到一个更加简洁高效的数字表达机制。
简化思维:如何用0-9表示所有的数字
现在,打出我们的小王牌,在牛顿亲切的关注下思考:
如何才能化复杂为简单呢?

已知:我们已经创造理解了0-9这十个符号,而且借助于手指这个自带形象化工具,理解十以内的数相对比较容易。
那么,思考一下:
我们能否用0-9这十个符号,来表达所有的数字。这样就实现了数字表达的简化,无需为每个数字创造一个符号。
顺着这个思路,如果我们要表示所有的数字。0-9可以直接表示,十根手指头如何表示呢?
简化思维:逢十化一
0表示没有,所以不能用0。接下来,就应该是1,我们能否尝试把十又变成1呢?
这就产生了「十进制」这个知识点。
同时,「逢十进一」这个动作,我们称之为「进位」。
这个1和以前的1肯定不一样。
但这样说太抽象了,又形成了复杂性难以理解。简化思维继续出场,如何能够简化我们的认知和理解呢?那就需要形象化。
从形象化的角度,类似于我们把10根棍子捆在一起,会形成一个更大的1。或者用手指的角度,类似于把两个手掌合拢在一起(10根手指),同时又是一个整体。
继续类推,如果有了10个10根在一起的棍子,又可以绑在一起形成更大的1。
这样对一堆棍子,总能变成1-9的数量(基于不同的单位)。
这样就从形象化的角度,解决了用0-9表示所有的数的问题(当然,一年级我们范围在自然数内)。
递归思维的应用
前面这种「逢十化一」,如果再次逢十继续化一的思路,我们称为「递归」。
在理科思维扑克中,递归性是方块10。

递归就像是俄罗斯套娃。一层套一层,你会发现同样的模式。
「没有什么问题是一包辣条不能解决的。如果有,那就再来一包」,这就是递归。
递归思维是一种重要的简化思路。它是「用一个方法来重复解决问题」。
简化思维:「位」的概念的诞生
但是问题没完,我们最后还要用数字表示。有些「1」显然单位更大,有些「1」单位更小,如何用数字来表示呢?
这就是「为了解决一个问题可能会产生新的问题」。
那么从直观的角度,可能有不同的方案。例如,我们可以把表示单位的,和表示数量的对应起来,做成表格。用形象化的符号表示单位是棍,还是捆,甚至捆的捆。
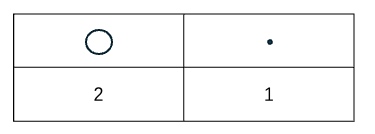
如果没有顺序的话,可能比较混乱。为了简化,我们规定,单位最小的在最右边(也就是1根的),接下来是10根一捆的......我们就很有秩序了。
就像班级排座位一样,最瘦的最右边,大家都有了自己的位置。这是数的位置,那就引出了「位」的概念知识点,进而有了对常见位的称呼「个位」、「十位」、「百位」。
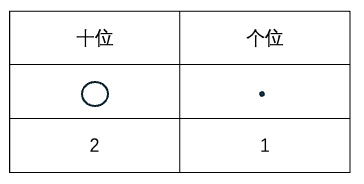
这种表示很完整,但占的地方大啊。
因为位是按照顺序固定的,所以我们熟悉之后,就可以去掉对位的形象化表示,和文字表示了,直接用数字「21」啦。这样进一步简化之后,就得到了我们日常的十进制表示法。
有序思维的应用
上面这种排序,其实就是一种「有序思维」的应用了。
主动的给数字建立秩序。
有序性在我们的扑克里,是方块J。

有限与无限:如何以有限破无穷
在哲学思想中,「有限与无限」是一个重要的话题。

在数学和现实中,也有很多重要的应用场景。
例如我们数的表示法,就是一个「有限破无穷」的问题。
如何用有限的数字符号,表示无穷的数?
在算术中,这才是真正的困难而重要的问题。
看上去是不懂38+25之类怎么计算,其实那只是表象。
真正的问题是,对十进制表示法,以及它更底层逻辑的缺乏认知。
刷题的必然失败:以有限的经验,应对无限的题型
大家应该都听过一句话:
吾生也有涯,而知也无涯
可能你认为这是鼓励你求知。
其实庄子后面还有一句:
以有涯随无涯,殆已
用有限的生命去追求无限的知识,你就完蛋了。
这也是一个「有限与无限」的辩证问题。
那怎么办呢?
我们难道不求知了吗?
你还是要求知,但是要超越狭隘的「应试题型」,去掌握底层逻辑,从而「以不变应万变」。
顶级高手之所以是高手,并不是因为他们「更熟练的刷题型」,而是高手根本不刷题型。
用思维能力破解难题
我们看前面十进制表示法的案例分析。
我们的红桃九是怎么来的呢?

为了解决「以有限符号表示无穷的数目」而发明产生。
而为了发明这个表达武器,涉及到几张不同花色的思维牌:
1)梅花6:有限与无限

2)小王:化繁为简

3)方块10:递归性
创造递归性(逢十化一)。

4)方块J:有序性
创造有序性(按照单位大小排序)

多张思维牌的组合,产生了十进制表示法这个伟大发明。
而它一旦发明,就成为了后续算术的基石。
这就是思维能力的力量。
然而在应试教育中,大家对这种力量一无所知。
所以费力不讨好。
学知识的思路:它是为了简化什么问题?
大多数同学学知识,就是记忆背诵做题。
但是要真正高效理解,并且化为自己的能力,你需要提问:
它是为了简化什么问题?这个问题的复杂性在哪里?
十进制是为了简化数的表示(后续还简化了数的计算)。
对数是为了简化乘法的计算,把乘法变成加法。
函数是为了简化我们对变化的事物或者关系的理解。
这样不光学会了知识,而且学到了解决问题的思路。
这就是「从少量的数据,挖掘出大量的信号」。
就像前面从十进制当中,我们就挖掘出了丰富的内涵。
你用这种学法,不看教辅,不用加班加点,不应试,已经可以吊打大多数同学了。
能管理更高的复杂性,意味着少走大量弯路
如果我们理解了十进制是为了解决更大的复杂性问题「如何用有限的符号表示无限的数」,不仅仅是理解了十进制概念本身,还意味着:
- 十进制加减法的复杂性大幅度降低,因为它们的复杂性很大程度源于十进制本身
- 巧算的理解难度和精通程度大幅度降低,因为小学巧算看上去各种模式,本质就是基于十进制的凑整
- 小数的复杂度大幅度降低,因为小数其实是十进制的分数
这样就无需大量刷题了,很快各种攻破。
还有一点,在数学课本的教学逻辑中,教学是一步一步的,例如20以内的数的表示和加减法、100以内的数的表示和加减法.....
在每个阶段都会刷大量的题目。
但如果你上手破解的复杂性就是「用有限的符号表示无限的数字」、「用通用的方法实现所有数的加减」,那么上来就已经了解了通用的数的表示法和加减法,无需按部就班学习什么「20以内的数」、「100以内的数的加减」之内。
因为「20以内的数」也好,「200以内的数」也好,都是「表示无限的数」的一种情况而已。
先掌握了通用的管理无限的数的复杂性的方法,那剩下的就简单了。
这就是为什么数学学习,非常强调「以通性求通解」。
也就意味着跳过了绝大多数的学习任务和刷题量。
而今天同学们每次都死记硬背新的知识点、刷题,效率极低,还掌握不好。
其实小学数学前三年的算术知识体系,用这种「攻克核心复杂性」的学习研究方式,一个月也就可以整体掌握了。剩下少量刷题来提升计算精准度也差不多了。
至于小学四到六年级的算术知识体系,再加一个月也够了。
然而学校的做法,就是让大家死记硬背,跳过了对真正复杂性的研究分析,脱离了数学教育的本质,没苦创造苦头让大家吃。
高手学习省力高效,靠的是降维打击
我们看学校里顶尖的同学,往往他们看上去没那么努力,有一种轻松通透感,刷题不多但是成绩稳定一流。
这种就是因为能够管理更高层次的复杂性,有更通用的底层能力之后,直接形成降维打击。
就像你在盘上公路上弯弯扭扭开来开去,人家直接上直升飞机。
他们的精力在哪里呢?
探索空气运动的规律、研发直升飞机。
你走再多的坑吃再多的苦,比不上去点更高的科技树。
在军事论坛讨论中,有一个常见话题是「两种战机格斗能力怎么样」。
然而在新时代的思想是「谁跟你斗狗?」,远程发射远距导弹干掉你就好了,缠斗不说明你厉害,说明你傻。
在5月的印巴空战,就是基于这种思想的经典案例。
当时数量上处于劣势的巴基斯坦空军,利用中国产的远程空对空导弹,和信息情报,在自身还处于印度飞机的打击范围之外时,发射导弹,导弹飞行150-200公里后击中印军战机,打了个6:0。印度空军连对手面都没见到,被打得蒙头转向收兵。
这就是降维打击。
各位以前反复应试刷题那是不知道,如果今天之后你还反复刷题,要想想「狗斗是证明我厉害呢,还是说明我傻逼?」
想清楚。
代数表示的基本演化
前面我们讨论了红桃J(符号表示)。

指出基于符号表示,在中小学算术代数中产生了最重要的两种表示:
1)算术领域:十进制表示法(数字符号)
2)代数领域:用字母表示数量(字母符号)
前面我们讨论了十进制表示法背后的思维,接下来让我们来看看代数表示法的思维和演进。
整体来说,中小学阶段代数表示法的演化是:
- 字母表示数量:最基本的符号表示(获得简洁表达通用性质的基本能力)
- 方程和不等式:表达洞察静态的数量关系
- 函数:表达洞察动态的变化关系
首先关于字母表示数本身,这个概念是容易理解的。
真正的意义,却被大家所忽视。
请注意我们解决问题,要「从复杂中求简单」,那么对应某种复杂性,一个恰当的表示,能够让我们简洁精确的看到现象、研究分析问题。
相比用具体的数字,使用字母表示数的核心意义在于,它解锁了「描述通用情况、发现通用规律」的能力。
例如,对于加法运算规律的研究,这种「研究规律」类的问题,本身就是通用性的。
你用23+25、73+285这种具体数字举例,从层次上是不匹配的,因为这些都是具体数字。
但是用 a + b 就很好了,这种抽象性对应着我们本身研究规律层次的通用性。
如果不用字母表示数,表达加法交换律可能要用一啪啦话,难懂。
但是 a + b = b + a 简单清晰。
这又是表达的力量。
那么这里问题就出来了, 这种力量,其实是当你研究规律的时候,才会发现它们的核心价值。
但是大多数同学在应试教育中,关注的普遍是「应用知识」,而不是「寻求规律」。
课本上那些知识,都是背下来的;刷的题目,通常都是求解具体问题,而非探索通用规律。
这样导致思维上跟不上,总是用「套用知识解题」思路。
回到前面的理科宪法第一条:爱智求真。

探索规律,是爱智求真的实践。
如果你本身思维是刷题求分,这种宏观思想就和数学以及整个理科观念不匹配,违宪。
于是各种不适应,看不懂。
这个看不懂不是个别知识层面了,是整体思路层面了。
例如初中上来,在有理数、多项式部分。
有理数当中会重新推导加法法则等,多项式中也是在代数情况下来应用四则运算法则产生规律性结论。
大多数同学并没有觉察到,为什么要这样干。
无非就是要考试。
这个天然就很难学好。
这就像恋爱里讲「化学反应」(chemstry)。
应试逻辑,和求真逻辑,是没法产生火花的。
就像很多人每天朝夕相处,产生不了理解,也产生不了爱情。
理解和爱情要有共鸣。
我们本身课本知识的逻辑,就是在研究规律中产生知识。
所以基于字母表示法,在有理数这个范围之内,我们开始推导研究规律。
首先基于已经知道的验证过的正数的四则运算规律,探索推导到有理数范围之内。
但这些还是针对两个数的一次加减乘除。
进一步推导探索更复杂的情况呢?
如果是多个数的四则运算呢(这时候数都用字母表示了)。
那不就是单项式和多项式,以及他们的规律了么?
还有,我们发现有多个乘法乘数相等的情况,想要简化一下表达,那就产生了乘方的概念。
这个思路对于有「研究规律、寻找通性」的理科思维的人来说,简直就是自然而言的,甚至不回去像。
本能就知道为什么要干这件事情,所以就自然的快速融入去把握思路了。
大多数人这时候都想着做题。
那你就完蛋了。
因为理科本来就是「掌握底层的规律,进而用规律解决各种问题」。
真正最难、最有价值的是第一步。
大家反而跳了。
在其实没多少技术含量的第二步雕花。
你解1000道382+235这种问题,都比不上发明十进制这一道题。
因为后者才是「解决通用问题」,前者只是后者重复一千遍。
而且解决十进制的发明问题,中间涉及到高阶思维的巧妙应用,这些才拉动思维能力。
这种「宪法共鸣」,是你和理科匹配的关键。
让我们来计算一下,为了十进制的计算,假设每个小朋友每天刷25道题,一年200天,就是5000道。两年算10000道。大多数时候是懵逼状态在刷。
至于吗?
搞懂十进制,刷1000道练手差不多了。
方程的伟大:实现了纯粹的「现象表示」
字母表示的另外一个产物,是方程。
我们的红桃Q。

方程的出现,实现了一个简化,就是让我们可以直接根据现象去表示现象。
这句话听上去是废话。
然而不是。
很多问题用算术方法,之所以困难,是因为你要产生一系列步骤,最后推出求解问题的结论。
例如鸡兔同笼。
但方程就不一样。他把解题分为两个步骤:
1)列方程
2)解方程
列方程,你不用管什么是条件,什么是问题了,大不了就设未知数。
用你所能理解的、简单的现象的逻辑列出方程。
然后用通用的方法求解。
这是我说的「根据现象去表示现象」。
一个伟大的发明。
因为简化了很多问题的求解难度,实现了「化繁为简」。

所以理科学习啊,不是说你知道了这个知识就行了,而是你了解了它怎么出来的,有什么厉害的地方,产生了什么价值。
因为这些,一方面才有理解、欣赏和热爱,一方面自己的知识和解题水平会截然不同。
函数的价值:表达与洞察变化关系
方程重点在于静态关系的表达。
而在现实中,有很多时候,是要关注连续变化的关系。
就像前面谈到的导弹发射,对方飞机一直在运动变化,这时候怎么表达时间和位置的关系?如何精准的预测判断?
这就是函数的用武之地了。

它给了我们对持续变化的关系的表达和洞察能力。
而函数又是物理的基本工具。
甚至「表达洞察变化关系」这个核心需求,很大就是从物理来的。
在理科思维扑克里,函数是红桃K,守护神是欧拉。
欧拉并不是第一个创造函数的人,但是他对函数做出了重要贡献,y=f(x)这个简洁的表达式,就是源于欧拉。
而在高中数学中,因为集合论的引入,函数的定义、运用等也跟着发生了变化。
初中数学,其大背景围绕「物理」展开,关注实用性。
而高中数学,其大背景是追求自身的进一步严谨,更关注逻辑性。
「集合」,就是这当中的一个关键。
集合的引入:数学的严谨性
高中数学和初中数学相比,一个核心变化,就是引入了集合,作为其它表示的基础。

这样就产生了各种衍生概念例如「解集」、「点集」、「集合运算」,在此基础上,很多初中的概念都被重新定义了一遍。
集合论产生的大背景,是在18世纪19世纪,数学家们觉得此前的数学不够严密,各种漏风。
康托尔创造了集合论,在此基础上把数学的严密性升级了。
然而,这样一来抽象性也升级了。
所以我们看高中数学,抽象度相比初中又高了一大截。
很多同学中考140多(满分150),到高中纷纷变成40分的零头。这和高中数学的抽象程度升级有很大关系。
如果我们梳理一下符号表示的核心演化脉络:
- 小学算术:十进制数字符号体系
- 初中代数:多项式、方程和函数代数符号体系
- 高中代数:基于集合论的方程、不等式和函数符号体系
这三套符号体系,造成了对大多数同学的理解挑战。
小学十进制,很多人凭借硬刷,花了几年的时间多少看上去过得去。
也是因为知识点少,奢侈让大家可以花几年时间攻克一个核心难点。
多项式、方程和函数符号体系,大多数同学玩不转了,靠刷题撑。
高中集合之后的升级版符号表示体系,彻底懵逼。刷都刷不动,不及格就是不及格。
我在高中的时候,有次数学老师说到集合的引入,是因为解决数学逻辑不严谨问题。
我当时听得觉得很重要。
但是大多数同学,对此毫无反应。
因为我从来就是用推导、分析、探索规律的方式去学习数学的,所以我知道「不严谨」这是什么意思?你首先需要建立在此前严谨推导分析的经验,才能站在这些经验上去体会「不严谨」。
大多数同学已经觉得初中代数、平面几何逻辑太强太抽象无法理解了,他们对「这还不严谨」根本是没有经验基础的。
应试教育不追求严谨,只追求提分。
真正的问题是,你要从头去理解这套符号体系的脉络。
掌握了脉络其实很简单。
自然而然的理解。
回顾:形象表达与抽象表达
回顾我们红桃(现象武器),13张牌如下:
- A: 现象的两种表达
- K: 函数
- Q: 方程与不等式
- J: 符号表示
- 10: 集合
- 9: 十进制表示法
- 8: 坐标系
- 7: 几何图形
- 6: 线段图
- 5: 数轴
- 4: 表格
- 3: 结构图
- 2: 示意图
这些牌的排序,大致是除了A,按照抽象表达到形象表达。
- K-9:抽象表达
- 8-2:形象表达
注意我前面谈到了,形象表达和抽象表达往往可能是融合的,所以可能一些牌既形象又抽象,这里只是按照主要特征大致分类。
前面整体我们讨论了抽象表达牌,接下来让我们看看形象表达牌的脉络。
几何图像:形象的抽象
在形象牌中,从数学角度最基础的是「几何图形」。
需要注意的是「几何图形」其实也是对「现实图形」的抽象。
因为我们是把现实图形的本质规律加以提炼,形成了几何图形。
就像前面泰勒斯对圆的定义,现实中很少有「到定点距离等于定长」的完美圆,多少有些出入,我们直接用理论定义了几何的圆。

关于柏拉图,我们都知道有个词叫做「柏拉图之恋」。
柏拉图之恋,并不是指男女之恋,而是指的是对永恒的纯粹的观念、真理的热爱。
他认为,现实世界的肉体是容易腐朽的,经验是短暂的、事物是不完美的。
你很难找到一个真正三条边是完美直线的三角形,然而在观念世界里,三角形完美的是三条直线边,内角和永远是180度。
只有在观念世界里,才有永恒、纯粹的真理。
从数学对象的角度,我们人类最早关注的,一个是数量,一个是空间形状。数字符号抽象了数量,几何图形抽象了形状。这两者也够成了数学基础。
一方面几何本身就是研究对象,一方面它很多时候又作为研究其它数学对象的工具。
同时,它所发展出来的一个独特用途,是基于这种直观性,做证明推理演绎几何,训练推理能力。
泰勒斯开创了对几何问题做数学证明,毕达哥拉斯学派发扬光大,而到了欧几里得则发展出平面推理几何。
关于欧几里得,在我们的梅花牌中会谈到他的「公理化体系」,这是学好初中推理几何的思想基础。
线段图:数量关系的直观表达
点和线算是最简单的图形元素,两点一线组成的线段,在数学中有了一个用途:对数量关系进行直观表达。
在小学阶段的解应用题中,线段图是头号武器。

在本章开头的家庭辅导案例中,关于这个题目:
小明家的鱼塘里养了草鱼、鲤鱼、鲢鱼和黑鱼,已知草鱼和鲤鱼一样多,黑鱼比草鱼少2条,鲢鱼比黑鱼多1条,鲤鱼有5条,问鱼塘里一共有多少条鱼?
我已经阐述了对小朋友难以理解题目的问题,有效破解,就是用线段图表达。
线段图看上去很简单,为什么家长们就想不到呢?
很多时候还是因为你不理解,为什么要用线段图,它解决什么问题。
今天有些学校,老师可能在小朋友开始接触应用题的时候,强制要求画线段图。一方面并不告诉大家为什么。
所以造成了一种奇观:有些时候没有必要学生在强行画线段图,有些时候线段图正好能解决问题,大家反而想不到。
线段图的广泛应用,是「数形结合」思维的体现。

它也是小学阶段最重要的数形结合工具。
而到了中学,数轴的重要性陡然提升。
数轴:从两点一线到无数点一线
线段是两点一线,数轴则是一条线上无数点(有一个特殊的点原点)。
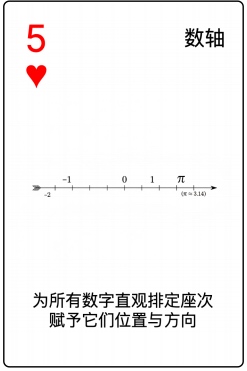
数轴和线段图不同。
线段图在数学中是一个辅助工具,我们常常用来解算术应用题时,用它表达数量关系。
然而不用,你能解出来,也可以。
但在中学数学中,数轴却是在代数基础知识体系的必需部分。
例如,在人教版初中教材中,我们对有理数大小的定义,就是直接从数轴来的(根据在数轴上的位置关系)。
数轴不是代数的外挂,而是代数的本体知识。
很多题目,要实现巧妙解决,往往都是利用数轴来做数形结合,例如求绝对值 、解不等式等等,数不胜数。
如果你是用理解推导的方式去学习思考,知道数轴的意义和在知识体系中的位置,这类数形结合转化往往是自然而言发生的。
但如果考刷题,少数同学刷多了能刷出经验,大多数同学刷多了其实还是没有敏感度。
但很多题,你有敏感度一眼就看出来(也就是后面方块会谈的线索能力),没有敏感度半天还搞不定。
这里谈到本体和外挂,其实如果你是基于理科宪法思想(爱智求真、化繁为简),往往学一遍就成了你的内生知识,自然懂了。
如果死记硬背灌输知识,想考刷题,哪怕刷熟练了也就是外挂,和你头脑自然的知识反应完全不是在一个层次。
所以顶尖同学往往是看见一道题本能就知道是什么知识点怎么解,马甲变了也无所谓;刷题的同学要靠手熟、过一段时间就要重新熟练刷熟,还不能变化太大要跟刷的题型长的差不多。长在自己知识体系中,和需要时候开外挂,是两回事。
两条数轴组合会发生什么呢?坐标系的登场
数轴非常重要,让我们来尝试围绕它做点文章探索。
我们用直线进行组合,会产生几何图形,例如三角形、长方形。
那么如果用数轴进行组合,会产生什么呢?
两个数轴围绕同一个原点,坐标系就产生了。
注意这两个数轴之间未必一定是直角,当然直角坐标系通常更简单、直观,成为了主流。
我们熟知的是笛卡尔发明了坐标系,其实费马也发明了坐标系,而且并不是限定直角的。
 费马本职工作是一位律师,业余爱好研究数学。他律师干得默默无闻,然而其业余爱好,却风生水起。
费马本职工作是一位律师,业余爱好研究数学。他律师干得默默无闻,然而其业余爱好,却风生水起。
他在一本丢番图的《算术》页边空白处,写下了一个猜想:「当整数n > 2时,关于x, y, z的方程 xⁿ + yⁿ = zⁿ 没有正整数解」。
然后说「我确实为此发现了一个美妙的证明,但这里的空白太小,写不下」,挖了个坑。
一直没有填上。
好奇心害死猫,数学家一直想他是怎么证明的。
过了350年,终于证明出来了。
这就是费马大定理。
回到坐标系。
数轴上的一个点,和一个有理数(实数)对应;那么两个数轴,每个数轴取一个点,最终就有了数对,同时在平面上指向一个点。
这样我们就有了一系列的武器和发现:
1)把平面上的点,和数对对应起来,这个数对也就是点的坐标
2)对于函数 y = f(x),如果数对一个点表示x,一个点表示y(也就是一条坐标轴表示x,一条表示y),那么我们就有了函数的图像,可以形象的看到函数的变化/映射趋势,函数的「形」的部分找到了,数形合体。
3)解方程和不等式,往往可以转化为和数轴或者其他线交点相关的问题,新的数形结合。
4)解析几何产生了,我们有了一种新的通用的方式,用代数来解决几何问题。很多以前难以搞定的几何推理问题,变成了代数搞定,不仅仅是非常强大的工具,诞生了一个新的学科领域。
5)一条数轴表示的正负数,最多只有两个方向(正/负)。而两条数轴组成的平面上的数,有很多方向。拓展对这种多方向的支持,向量产生了。进一步产生了向量的运算。这又成了超级强大的工具。
6)在古希腊时代那些哲学家,就开始研究圆锥曲线。解析几何之后,大家发现这些曲线其实就是一些函数的图像,这样代数和几何、古代和近代又产生了奇妙的联系。
初中到高中很多知识和题目,就是在这些领域上变化花样。
把握了脉络,其实很多事情就简单。
三条到多条数轴会发生什么呢?高维空间与人工智能
那么,如果再增加一条与x轴、y轴都垂直的数轴(z轴),会发生什么呢?
我们就从二维的「平面」,进入了三维的「空间」。一个点的位置,不再由(x, y)这两个数决定,而是由(x, y, z)这三个数组成的「数组」来精确定位。这,就是我们在物理课上描述物体运动、在电脑游戏中构建虚拟世界所依赖的三维直角坐标系。
到这里,我们的想象力似乎已经到了极限,因为我们生活在一个三维空间里。
但数学家和科学家的思想,从未被我们的肉眼所束缚。他们问了一个更疯狂的问题:如果,组成这个「数组」的数字,不是3个,而是几百个、甚至几千个呢?
这就诞生了「高维空间」的概念。它在物理上无法被看见,但在数学上,它真实存在。而这个看似天马行空的思想,在今天的人工智能(AI)领域,爆发出了惊人的力量。
比如,AI如何「理解」我们人类的语言?它使用一种叫做「词向量 (Word Embedding)」的技术。简单来说,它会为每一个词,比如「国王」、「女王」、「男人」、「女人」,都生成一个由几百个数字组成的「高维坐标」。
在这个由AI构建的、我们看不见的「语言空间」里,奇迹发生了:
语义的远近,变成了空间的距离。 比如,「国王」这个点,和「女王」这个点的空间距离,会非常近;而和「香蕉」这个点的距离,就会非常远。
语义的关系,变成了空间的方向。 甚至可以发现,从「国王」这个点,走向「女王」这个点的「方向和距离」,与从「男人」走向「女人」的「方向和距离」,几乎是完全一样的!我们甚至能通过向量运算,得出 「国王」 - 「男人」 + 「女人」 ≈ 「女王」 这样令人震惊的结果。
从简单的直线和点出发,通过不断的组合与升维,我们最终抵达了人工智能的核心腹地。这,就是数学表达的力量。它不仅在描述我们已知的世界,更在构建我们未知的未来。
总结:现象武器与表达能力
回顾我们红桃(现象武器),13张牌如下:
- A: 现象的两种表达
- K: 函数
- Q: 方程与不等式
- J: 符号表示
- 10: 集合
- 9: 十进制表示法
- 8: 坐标系
- 7: 几何图形
- 6: 线段图
- 5: 数轴
- 4: 表格
- 3: 结构图
- 2: 示意图
红桃A是整个红桃的统领牌,它指出了两种表达:形象与抽象。

这些牌的排序,大致是除了A,按照抽象表达到形象表达。
- K-9:抽象表达
- 8-2:形象表达
注意我前面谈到了,形象表达和抽象表达往往可能是融合的,所以可能一些牌既形象又抽象,这里只是按照主要特征大致分类。
把握了这些武器的意义和演化逻辑,从小学到高中的核心知识,其实很大程度已经打通了。做题,也就能选择「恰如其当的表示」。
从能力角度,红桃代表了「表达能力」。
跟语文、显示工作和生活一样,能够清晰的、恰当的、精准的表达现象,是非常高价值的、很稀缺的能力。
有效的表达,那么直接破除迷雾搞定,要么为后续的研究奠定基础。
在此基础之上,就要动用「线索武器」了。