第四章:黑桃(策略武器)
从数理思维到通用智慧
回顾我们理科思维扑克牌的结构:
1)两张王牌、两条宪法
- 大王🌟 (爱智求真)
- 小王🪄 (化繁为简)
2)四种武器、四大能力
- 红桃♥️ (现象武器): 表达能力
- 方块♦️ (线索武器): 观察能力
- 黑桃♠️ (策略武器): 谋略能力
- 梅花♣️ (规律武器): 哲思能力
前面我们讨论了红桃和方块。
整体来说,绝大多数红桃和方块牌,主要还是在数理学科的范围之内。
而接下来的黑桃和梅花,会有重要的差异,这两者的核心牌,基本上都是「通用智慧」,高度跨领域。
通用智慧可以粗略分为两大部分:
- 认知智慧:深度的本质洞察
- 实践智慧:高超的策略水平
我们的黑桃对应着实践智慧,梅花对应着认知智慧。
当然这两者其实是相辅相成,实践是how,认知是why & what,所以顶尖的高手,通常是两种智慧的融合,认知与实践打通。
也因此,大家在黑桃和梅花上,要注意以数理学科为手段,以修炼通用智慧为目的。
最高的策略智慧:孙子兵法
统领策略牌的黑桃A,守护神是孙子,战略学的祖师爷。

谈策略就就谈「孙子兵法」。
孙子兵法,成书于春秋时代。一直到今天,依然是世界顶尖的战略著述。
学者曾经怀疑,这本书是后人伪作。因为在那个时代,几乎所有著作,都是散文集,缺乏严密的内在结构。而「孙子兵法」不同,全书可以分为几个大的部分,逻辑缜密,环环相扣。单纯从这一点,已经超越了那个时代。
一直到山东银雀山的考古发现,才确定孙子兵法并非后人的伪作。
而孙子的战略思想,更远远超越了那个时代,也超越了单纯的军事范畴。在美国亚马逊上,它的英文版,是哲学类排名第一的畅销书。
孙子战略思维中最重要的部分,是「全胜思维」。用他自己的话说,是「必以全争于天下」。
那么到底什么是「全」呢?要理解这一点,首先要理解「用兵之害」。
凡用兵之法,驰车千驷,革车千乘,带甲十万,千里馈粮,则内外之费,宾客之用,胶漆之材,车甲之奉,日费千金,然后十万之师举矣。
其用战也胜,久则钝兵挫锐,攻城则力屈,久暴师则国用不足。夫钝兵挫锐,屈力殚货,则诸侯乘其弊而起,虽有智者,不能善其后矣。故兵闻拙速,未睹巧之久也。夫兵久而国利者,未之有也。故不尽知用兵之害者,则不能尽知用兵之利也。
......
故兵贵胜,不贵久。故知兵之将,生民之司命,国家安危之主也。
应试教育,就是典型的「钝兵挫锐」。学生天天都在学习,晚上还要加班加点。看上去努力,其实人都疲了,士气低落,效率不高。而且这种情况持续,还可能造成严重的心理问题,也占用了大量时间精力,难以让学生有生活、有发展。
那到底应该怎么办呢?孙子提出了他的见解:
夫用兵之法,全国为上,破国次之,全军为上,破军次之;全旅为上,破旅次之;全卒为上,破卒次之;全伍为上,破伍次之。是故百战百胜,非善之善者也;不战而屈人之兵,善之善者也。
故上兵伐谋,其次伐交,其次伐兵,其下攻城。攻城之法为不得已。修橹轒辒,具器械,三月而后成,距堙,又三月而后已。将不胜其忿而蚁附之,杀士三分之一而城不拔者,此攻之灾也。
故善用兵者,屈人之兵而非战也,拔人之城而非攻也,毁人之国而非久也,必以全争于天下。故兵不顿而利可全,此谋攻之法也。
孙子说「上兵伐谋」,要「兵不顿而利可全」。兵不顿,是低成本;利可全,是高收益。这两者结合,就是「全胜」。
这也是一种投资视角。
兵不顿,是低成本;利可全,是高收益。学习跟打仗一样,要算账,要成本低收益高。
不要亏本。
天天刷题的同学,亏死了。
我们要「全胜」,要「上兵伐谋」。
那么最重要的谋略有哪些呢?
如何化繁为简?简化的5大策略
回顾我们的小王,理科宪法第二条「化繁为简」。

探索真相,都是要围绕「对复杂性有效简化」。
那么具体如何简化?
有5种最重要的简化策略。
这5项策略,并不是数学领域的专属,而是本质上源于人类和世界交互的5个核心行为。因为它是各个领域,求得真相解决问题的利器。
概要的说,人类和世界,有5种基本交互:
- 适应世界
- 感受世界
- 理解世界
- 连接世界
- 改变世界
对应这5种交互,有5大核心策略。它们成为了「求真五星旗」的5颗星。

| 起源 | 策略 | 核心定义 |
|---|---|---|
| 适应世界 | 演化策略 | 通过从最简单、最特殊的案例入手,遵循事物演化规律,逐步推演。 |
| 感受世界 | 形象策略 | 通过图形、空间、比喻和物理直觉等形象化方式感受事物。 |
| 理解世界 | 抽象策略 | 通过符号、规则、原理、模型和公理等抽象方式来理解事物。 |
| 连接世界 | 转化策略 | 转化事物、转化概念、转化方向、转化视角 |
| 改变世界 | 创新策略 | 设定新的规则、标准,创造新的事物和场景 |
解决任何难题,破解各种迷雾,往往都是基于这5种核心策略和组合,来落实简化。
黑桃K:演化策略
演化策略的守护神,是笛卡尔。

在数学史上,笛卡尔发明了坐标系,创造了解析几何。
这背后,是他深厚的底层智慧。
笛卡尔非常重视演绎策略,他在《谈谈方法》中说:
从最简单、最容易认识的对象开始,一点一点、一步一步上升到对最复杂对象的认识。
这简直是演化策略的标准定义。
但只是一半,因为他重点谈认知。
这是认知的一半。
实践角度,演化策略就是从基本的、最简单的开始,一步步推进。
一样的逻辑。
继续用「鸡兔同笼」为例:
鸡兔同笼,共38个头,112只脚,那么鸡有多少只?兔有多少只?
我们在「王炸」部分分享的简化思路,其实应用的就是演化策略:
这题目我们没见过没做过,怎么思考呢?
好像做不出来呀,太复杂了。
我们能不能【简化】呢?从题目中【简化】出我们能做的,然后看看如何逼近到最终的问题?
那么,这道题的【复杂性】在哪里呢?
因为又有鸡又有兔子,很难计算,无从下手。
要是【简化】的话,就应该是只有一种动物,这样简单很多。【演化:最简单的情况】
那么我们假设笼子里只有鸡,一共38个头的话,就应该有38只鸡。
每只鸡两只脚,那就是76只脚。
然而题目里一共是112只脚。差了36只。
这个差异怎么来的呢?有些兔子被我们假设成鸡了。
那么到底有多少兔子呢?
这个比较复杂,难以想清楚,我们就一步一步来嘛【演化思维】。
目前我们假设所有都是鸡,没有兔子。
那么我们走出一小步,如果有一只兔子呢?【演化:从没有兔子到一只兔子】
这时候应该是37 x 2 + 1 x 4 = 78只脚。
或者,因为少了一个兔子多了一只鸡,而兔子比鸡要多了两只脚,所以应该是76 + 2 = 78只。
如果有两只兔子呢?那就应该是 78 + 2 = 80只。【演化:从一只兔子到两只兔子】
这样我们也就能找到规律了。
每用一个兔子换掉一只鸡,就会多出两个脚。
而目前我们差异是36只脚,36 / 2 = 18。
应该有18只兔子,而鸡是 38 - 18 = 20只。
验算一下: 2 x 20 + 4 x 18 = 40 + 72 = 112只。
正确。
在这个解题思路中,我们基于「演化策略」,实现了一步步演化:
- 研究没有兔子的情况
- 研究一只兔子情况
- 研究两只兔子情况
从线索的角度,其实这里用到了「特殊值线索发掘」。前面已经讲过了。
所以各种牌其实有相互关系,往往组合运用。或者多个角度,都能产生思路。
演化策略之所以有效,因为它遵循的是最基本的事物/认知发展规律。
然而在应试教育中,普遍违背了演化规律。
例如,你要先理解基础知识,然后才能刷题巩固知识。
应试学习不关注基础知识理解,让大家死记硬背,强行刷题。
跳步了。
一楼都没修就修二三楼。
所以非常愚蠢。
一问就是「如果你不行,那就多刷题」。
没有有效的策略,只有蛮干。
基于演化策略,当问题太复杂的时候,你需要循序渐进的解决,不能一口吃个胖子。而且要从此前的经验中沉淀和借力。
笛卡尔说:
我所解决的每一个问题都将成为一个范例,以用于解决其它问题。
他还说:
如果我在科学上发现了什么新的真理,我总可以说它们是建立在五六个已成功解决的问题上;它们也可以看成是五六次战役的结果,在每次战役中,命运之神总是跟我在一起。
高手往往是复利很高,他们的整个学习研究过程就是在持续演化,能够从一次胜利走向下一次胜利,步步高。
反过来应试学习,大家看上去很拼命,其实这些刷题、或者上课的各种行为之间,很少有演化承接的逻辑,总是在一楼死记硬背从头干,所以费力不讨好。
这就像打牌,菜鸟打一张牌往往就是应对当前的局面,被动而零散。高手是对局势有一个整体的判断和规划,打牌是在为后面的打基础,让局势演化到自己期望的逻辑,整体就是一条演化路径。
所以不要看你有多努力,光努力是成本,不是收益。关键你是不是规划演化的路径和终局,并且付诸实现。
黑桃Q:形象策略
黑桃Q和J,分别是形象策略和抽象策略。
大家还记得我们现象的红桃A吗?
其中指出两种表达:

形象表达和抽象表达,其实可以认为是源于「形象策略」和「抽象策略」,在表达方面的具体化。
形象和抽象本身就是辩证关系,相辅相成,经常共同出现。
让我们先看形象策略:

形象策略的守护神,是麦克斯韦。
1856年2月,麦克斯韦在剑桥哲学学报上发表了第一篇电磁学论文《论法拉第力线》,他环顾了当时电磁学研究的现状,指出虽然已经建立了很多实验定律和数学理论,但未能揭示各种电磁现象之间的联系,他写道:「电科学的现状看来特别不便于思索。」
他认为:
有效的科学研究的第一步,必须把已有的研究成果简化和归纳成一种思维易于领会的形式。
而形象化往往会让思维容易理解。
麦克斯韦的天才之处,在于他拥有一种将极其抽象的数学,与极其具体的物理形象,进行无缝连接的非凡能力。
当时,法拉第通过实验,已经提出了「力线」这个形象化的概念,来描述电场和磁场。但这些「力线」,在很多数学家看来,只是一个粗糙的比喻,不够严谨。
而麦克斯韦,非但没有抛弃这个「形象」,反而将它推向了极致。他开始想象:
- 如果这些「力线」,是一种真实存在的、像流体一样在空间中流动的「以太」呢?
- 如果磁力线,是这个流体中正在旋转的「小涡旋」呢?
- 如果两个涡旋直接接触会摩擦损耗,那么在它们之间,是不是应该有一些像「滚珠轴承」一样的小颗粒(他称之为「电粒子」),来让它们顺畅地转动呢?
他在脑中构建的,就是这样一个充满了齿轮、涡旋、滚珠的、极其复杂的、维多利亚时代蒸汽朋克风格的「宇宙机械模型」。
正是基于这个极其大胆、极其形象化的物理直觉,他开始进行数学推导。奇迹发生了——这个看似荒诞的模型,竟然完美地推导出了一组可以统一电、磁、光所有现象的、有史以来最深刻的数学方程组——麦克斯韦方程组。
麦克斯韦用他的实践证明:最深刻的抽象,可能就隐藏在最大胆的形象之中。
在数学课本中,关于抽象策略的应用比比皆是。毕竟我们课本的一个核心,就是从现象中提炼抽象本质规律。大家顺着这个思路,理解课本就容易。
那么,形象思维如何用到解题中呢?
还是用鸡兔同笼为例:
鸡兔同笼,共38个头,112只脚,那么鸡有多少只?兔有多少只?
让我们考虑采用一个常用的现象武器:线段图。
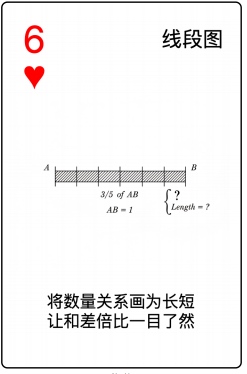
目的:通过画线段图直接的看到关系。
这道题画线段图还是有点难度的,没那么直接。
我们如果用通常小学阶段线段图的画法,例如首先分别把鸡和兔的总脚数看看能不能画出来?
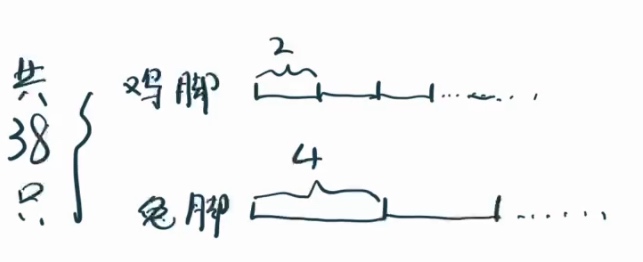
画起来很尴尬,因为鸡的数量和兔子数量都不知道,两条线都没法合拢。
另外一方面,鸡兔一共38只这个条件,在线段中没有用上。
所以现在问题来了,我们怎么能把一共38只这个条件用上去呢?
这时候你要进一步分析了。
为什么38用不上呢?
如何能够用上38呢?
核心是鸡和兔脚数量不一样。
基于简化思路,能不能尝试让鸡和兔脚一样呢?
我们如果把兔子的脚只拿两只出来,另外两只当替补,好像就可以了吗?
甚至我们可以造一个概念(这个是为了更容易自己理解,没这个概念也行),那就是每只兔子4只脚,两只主力上场,两只替补候选。
这样我们从不相等,制造了一个相等。
鸡两只脚都是主力,没有替补。
主力可以一起打比赛了,对等了。
甚至这个题,你可以进一步形象化,问自己,为什么鸡脚和兔脚数量不一样?
鸡有两只爪子,两个翅膀,翅膀不能算脚,因为不粘地。
兔子两个前脚,两个后脚。
那么我们可以把鸡的爪子叫做后脚,翅膀叫做前脚(进化了,不占地了)。
这也会产生一个同样的概念和相等的,后脚。
其实这些都是便于理解形象,核心是从简化出发,把兔子的脚做个分离,产生两只脚,这样可以跟鸡脚相等。进一步可以发挥我们这个一共38只的条件。
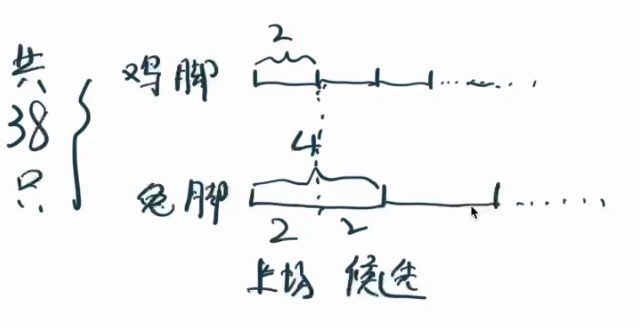
那么怎么发挥呢?
其实这就是创造了一个不变性线索:兔子的主力脚(2只)是和鸡的主力脚(2只)相等的。
没有不变性,创造不变性。

那么我们主力部分一共多少脚呢?这就是确定性了,反正无论如何每个动物都是2只脚。也就是说,每只动物的主力脚数量守恒,可以简化问题。
画线段图可以把主力脚部分完整的画出来。
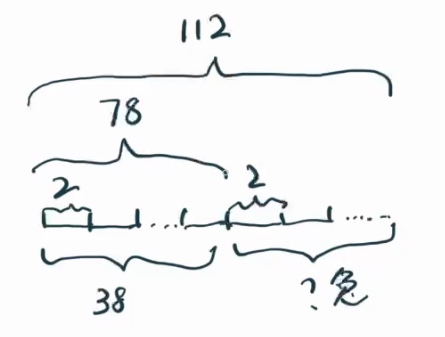
而剩下的,就是兔子的「替补脚」,这样画图就可以画了。
只有一个未知数量。
搞定收工。
形象策略是非常强的策略,因为它契合了我们的感官、现实经验。
和其它牌组合,更能发挥其威力。
黑桃J:抽象策略
形象策略是要贴近现实、我们的感觉。
而抽象策略反过来,则是要抽离表面因素,提炼纯粹的本质。

抽象策略的守护神,是乔布·布尔。
乔治·布尔是19世纪的英国数学家,他堪称是「将思想本身,变成数学」的第一人。
在他之前,代数是用来研究「数」与「量」的。而布尔,提出了一个石破天惊的想法:代数,为什么不能用来研究「思想」和「逻辑」本身呢?
他做的,就是一次终极的「抽象」。
他将我们日常语言中那些复杂的、充满了感情色彩的逻辑判断,「滤去」了所有的具体内容,只提炼出其最纯粹的、非黑即白的内核。
他规定,任何一个命题,无论它多么复杂,其最终的「真值」,都只有两种可能:「真」(用 1 表示)或「假」(用 0 表示)。
他将逻辑关系中的「与」(AND)、「或」(OR)、「非」(NOT),完全等价于代数中的运算。比如,「A与B同时为真」,就等价于 A x B = 1。
这,就是布尔代数的诞生。
布尔的伟大之处在于,他将人类最复杂的思想活动,抽象成了一套可以用0和1进行运算的、极其简单的符号系统。
这个看似「无用」的、纯粹的抽象游戏,在一个世纪后,成为了整个数字计算机和信息时代的逻辑基石。你每一次在搜索引擎中敲下关键词,每一次计算机执行「如果-那么」的判断,其背后,都是布尔的思想在低语。
回到我们日常的学习。
我们看课本的各种知识,很多都是在抽象。因为本质上数学课本做的一个核心事情,就是从现实中抽象出本质规律。
你读课本,也就要顺着这条线索去进行提炼抽象。死记硬背没用。
那么如何用抽象思维解题呢?
还是用鸡兔同笼为例。
这道题,我们被鸡和兔子困扰,但是「鸡」和「兔子」真的对解题重要吗?如果换成「鸭子」和「猪」题目会有差异吗?
并没有。
那么既然如此,「鸡」和「兔子」只是一个表述,真正的问题在于更高层次的抽象关系。
那么我们能否抽象到更高层次,摆脱形象的干扰来解决问题呢?
我们可以使用通用的数学符号(如变量x和y)来代表它们的数量,然后用严谨的数学方程式来描述它们之间的关系。这是一种将具体问题升维到纯粹符号世界的路径。

这个大家都会,我不列方程了。
黑桃10:转化策略
转化策略的方向包括:转化事物、转化概念、转化方向、转化视角。
其核心,是通过转化来简化问题,从而高效处理。

转化策略的守护神,是约翰·纳皮尔。
约翰·纳皮尔是16世纪的苏格兰数学家。在那个「大航海时代」,天文学家、航海家和工程师们,每天都面临着一个巨大的、令人头痛的敌人——繁琐的计算。
尤其是涉及到超大数字的乘法、除法和开方运算,不仅耗时极长,而且极易出错。一个微小的计算失误,就可能导致一艘船偏离航线几百公里。
纳皮尔花了二十年的时间,去思考一个革命性的问题:
有没有一种魔法,可以将复杂的『乘除』运算,『转化』成简单的『加减』运算?
他发明了一套全新的数学工具——「对数」(Logarithm)。
对数的神奇之处,就在于它真的实现了那种「魔法」般的转化:
- log(A × B) 等价于 log(A) + log(B)
- log(A ÷ B) 等价于 log(A) - log(B)
这意味着,任何两个大数的乘法,都可以被转化为「查对数表,然后做一次简单的加法」。
纳皮尔的这项发明,被誉为「将天文学家的寿命延长了一倍」。它将无数的科学家和工程师,从计算的地狱中解放了出来,极大地推动了科学革命的进程。
当你觉得眼前的道路无比艰难时,不要硬闯。试着去寻找一条平行的、更简单的「等价」路径,然后优雅地「转化」过去。
转化策略,往往是基于对「等价关系」线索的发现。

例如纳皮尔,他用对数把乘除运算转化为加减运算,利用的是乘除法到加减法的等价性。
而前面我们谈到的毕达哥拉斯定理的证明,利用的是面积和乘法的等价性。
在介绍毕达哥拉斯定理的证明思路之后,我留了一个问题:
能否参考毕达哥拉斯定理证明思路,来解决鸡兔同笼问题呢?
那我们来看看,这个思路是怎样的。
我们看鸡兔同笼这道题。
鸡兔同笼,共38个头,112只脚,那么鸡有多少只?兔有多少只?
从38个头,我们可以很快理解到,鸡兔一共38只。因为两者都是一个头。
迷雾在于鸡和兔的数量未知、而两者脚数量不一样。
鸡有两只脚、兔有四只脚。
那么这个能观察出什么呢?
一只兔子的脚数量,是鸡的两倍。
前面我们谈高斯的案例,高斯观察到数列前后的对称性,快速解出了1+2+3...+n的和。
高手有一种特征和敏感,就是善于在复杂问题中,观察出相对简单、特殊的特征,然后尝试作为突破口。
那么「兔脚是鸡数量的两倍」,是不是可以做文章呢?
回到我们「转化思路」,这个可以如何转化呢?
我们进一步观察兔脚和鸡脚,4和2。
4很有意思,它是一个完全平方数。
完全平方数有什么几何意义呢?正方形面积。
2x2的正方形的面积。
那么2代表什么呢?
2x1的长方形面积。
两个长方形拼起来就成了正方形。
联想:经典的勾股定理的证明,$ a^2 + b^2 = c^2 $,一种思路就是转化为面积求证。
那么我们是否可以这个脚数转化为面积,这样应该会产生新的题目。
而长方形和正方形,貌似要比鸡兔同笼直观很多。
从这个思路,我们可以产生一道等价的题目:
长方形和正方形一共38个,长方形是1x2,正方形是2x2,总面积为112,请问有多少长方形、多少正方形。
这个我们设定都是正方形,那么112/4=28个。
但是一共是38个,为什么呢?一些正方形分成长方形了呗。
每把一个正方形拆成长方形,面积保持不变,但是会多一个图形。
从28到38,意味着拆了10个正方形。
所以就是20个长方形。
还有18个正方形。
好啦,这道等价的求图形个数的题目,算起来就直观多了。
这样,我们抓住4/2倍数关系,进一步观察发现4的完全平方数性质,从这方面入手(可能联系到勾股定理证明来强化我们的方向思路,当然也可能联想到其它题目,或者没有联想直接干),把「脚的数量」转化成了「图形面积」,把「求动物个数」转化成「求图形个数」,用更直观的方式解决了问题。
顶级高手的特征:跨领域的举一反三融会贯通
这个「把鸡兔同笼转化为几何问题」的解法,是一个大范围跨领域的迁移。
我们把算术问题转化成了几何问题,这是一个大范围迁移。
我们联想到勾股定理的求面积解法,把勾股定理的证明思路迁移到鸡兔同笼这个看上去风牛马不相及的题目上,这也是大范围迁移。
这是一种顶级高手的能力,掌握底层逻辑之后实现跨领域迁移。
这也是为什么高手往往不用刷题型,就很厉害。
没有这种题型的经验,他们可以用你看上去截然不相关的题目中获得的经验来触类旁通。非常善于转化,把一个问题转化为另一个问题,从一个视角转化到另一个视角。
乔布斯说:
创造力只不过是把事物关联在一起而已。如果你问有创造力的人是怎么做出东西来的,如何做成某件事的时候,他们会有一点愧疚。因为他们并没有真正「做」东西,他们只是能「看到」东西。一段时间之后怎么做就会变得非常明显。这是因为他们能把自己的经验和新东西综合起来。因为他们拥有比别人更多的经验,他们对自己的经验想的更多。
但是「题型专家」就不行了。
因为题型专家,总结题型就是靠「表面现象」,例如题目条件的类型、应用模型等等,而并不关注「底层关系和逻辑」。
我上次看到一位家长帮孩子梳理「植树类问题」,从三种基本情况「两边都植树、一边植树、两边都不植」,拓展出10多种变型。
归纳很详细,每种都要做例题。
小朋友也真做了。
妈呀,解题不是这样靠归纳法详细到脚趾头的,这样累死了。
而且家长干了很多活,小朋友也辛苦。
这一章要归纳,下一章还要归纳,要做那么多题。
这是一条苦逼的道路。
不要吃苦,要享福。
死记硬背本来就没把研究和创造力当回事,总想套现象。
表面现象是没办法跨范围迁移的。
只有底层逻辑才是通用的。
所以高手掌握「简化的底层逻辑」,灵活的应用到各个领域;菜鸟刷了无数题,成为了众多「表面题型」的专家,还是很菜。
还有,菜鸟刷题题型都是基于「应试」的,所以离开应试往往毛用都没有;但是「化繁为简」的底层逻辑不光是数学通用、物理通用,对工作和人生往往也是通用的。
这样,以不变应万变,庖丁解牛游刃有余。
黑桃9: 创新策略
创新策略,就要设定新规则、新标准。

我们继续看鸡兔同笼这道题。
鸡兔同笼,共38个头,112只脚,那么鸡有多少只?兔有多少只?
让我们先回到复杂性「又有鸡又有兔子,数量都未知,脚数不一样,比较复杂」。
那么,我们能否设定新的规则,实现简化呢?
脚数不一样,能否让脚数一样呢?
什么情况脚数才能一样?
一种情况是:「鸡兔是配对的」,这样一对总是6只脚。
这个思路好像有点意思,顺着思考,如果这样的话,最终就是两组动物:
1)配对的鸡兔
2)落单的鸡或者兔子
那么落单的是鸡还是兔子呢?还不知道。
如果正好38只配对的话,那么就是19对,每队6脚,就是114脚。
哎呀,但是题目是112脚,这个很接近了,但是差了2只。
很接近了,说明没有完全配对,但很近了,应该是18对,用18套进去,算一下还有两只兔子,验算正确。
这样通过设定新的规则,简化问题看到真相。
顶级的高手,深刻掌握了简化的底层逻辑
回到前面我们谈到的「求真5星旗」(5大减缓策略):
| 起源 | 策略 | 核心定义 |
|---|---|---|
| 适应世界 | 演化策略 | 通过从最简单、最特殊的案例入手,遵循事物演化规律,逐步推演。 |
| 感受世界 | 形象策略 | 通过图形、空间、比喻和物理直觉等形象化方式感受事物。 |
| 理解世界 | 抽象策略 | 通过符号、规则、原理、模型和公理等抽象方式来理解事物。 |
| 连接世界 | 转化策略 | 转化事物、转化概念、转化方向、转化视角 |
| 改变世界 | 创新策略 | 设定新的规则、标准,创造新的事物和场景 |
我用鸡兔同笼的案例,给大家演示了如何从这5种策略出发,分别产生一种解题思路。
而真正解题的过程中,这些策略往往又会组合使用。例如转化策略的「转化为面积」,其实也是「形象策略」的体现,同时也是抽象策略的体现(因为脱离了鸡兔的表象,抽象了实质的数量关系)。
顶尖的高手,非常擅长用这5种策略去分析和处理问题,尽管他们往往是无意识的。
通过有意识的训练,你可以高效的来提升自己的简化能力,成为「化复杂为简单」的高手。
接下来的黑桃牌8-2,是更具体落实这5大简化策略的重要战术武器。
- ♠️8: 数形结合
- ♠️7: 分而治之
- ♠️6: 升维打击
- ♠️5: 构造法
- ♠️4: 等价变形
- ♠️3: 反证法
- ♠️2: 倒推法
黑桃8: 数形结合
数形结合是数学中非常重要的一种策略。
本书中已经大量篇幅和它相关。
它其实是形象策略、抽象策略、转化策略的进一步落实。
「形象策略、抽象策略、转化策略」,都是通用智慧,跨领域的。
而数形结合,则是把「通用智慧的策略原则,和数学领域的具体特征结合」。
在层次上低一些。

数形结合的守护神是华罗庚,他讲过一句著名的话:
数形结合千般好,隔裂分家万事休
真的如此。
大家数学学习要形成本能,遇到数去思考寻找它的形,遇到形思考寻找它的数(代数)。
鉴于本书一堆案例都和它相关,不再举例。
黑桃7: 分而治之
分而治之是一个非常常用的策略。
当问题比较复杂,我们就分解为更小的问题,然后逐个击破。
这也是一种演化策略的思路。
分类讨论就是在分而治之。

分而治之一个难点在于,如何有效的分类或者拆解,让拆解出来的问题结构本身容易被处理、简单。
这很大程度跟观察判断有关系。
例如在方块中「有序性」谈到的数三角形个数的例子:
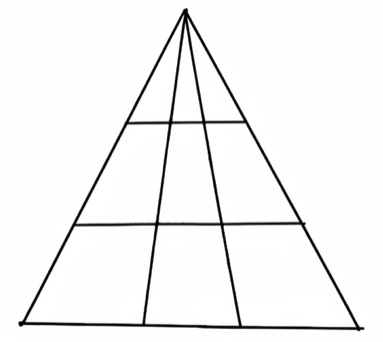
重点是找到/创造一个有序的结构,这个结构本身就容易让我们逐步分情况数清楚。
关于分而治之执行本身,更多的是严谨细致。
不多谈了。
黑桃6: 升维打击
升维打击是一种非常重要、反常规的思路。
属于创新策略的一种思路。
它的核心思想是:
如果你难以解决一个问题,那么去解决比它更普遍、更高层、更深刻、往往看上去也更困难的问题。解决了更大问题之后,手头问题自然迎刃而解。
它的反常识在于,我们遇到了难题,通常思路是一步一步来,从更小的研究。
而这个则是「干脆干一票更大的,顺便就把手头的搞定了」。
举个例子,假设我们要解 $ 2x^2 + 8x + 5 = 0 $,我们不会解。
那怎么办呢?
升维打击思路就是,我们能否找到 $ax^2 + bx + c =0$的通用解法呢?如果找到了,自然我们就把手头的问题解决了。
这样看,也不是那么不可思议是吧。
为了把醋给用了,那就包个饺子。
为了吃口热饭,干脆就发明个微波炉。

在理科思维扑克中,「升维打击」是黑桃6,它的守护神,正是这种「微波炉思想」的终极大师——黎曼。
黎曼之前的数学家,包括他的老师高斯,都在研究我们能看见的、三维空间里的二维曲面(比如球面、马鞍面)。这是一个复杂的问题。
但黎曼的反常规之处在于,他没有去解决这个或那个具体的曲面问题。他问了一个更疯狂的问题:「我们能不能创造一种,可以在任意维度(四维、五维、甚至N维)空间里,都普遍适用的几何学?」
他要解决的,是一个比所有人都更普遍、更高层、也更困难的问题。最终,他成功创造了「黎曼几何」。
这套理论,在当时就像一把过于超前的屠龙刀,看上去厉害,但是没龙可杀。
半个多世纪后,爱因斯坦在创立广义相对论时,苦于无法用数学描述弯曲的「四维时空」,才发现,黎曼炼的屠龙刀真棒,他的感觉就跟孙悟空拿到金箍棒一样「终于有了个趁手的兵器」,然后打出了惊天一击。
这就是「升维打击」的威力。当你被眼前的难题困住时,不妨抬起头,去思考一下:有没有一个更大的、更普遍的问题,一旦解决了它,眼前这个小麻烦,就会自动烟消云散?
对于同学而言,我觉得最需要升维打击的,是刷题问题。
今天大家普遍刷题,大家想要解决的,是「刷题效率问题」:
我能不能刷题更高效一些,正确率高一些,错误订正更精确一些。
如果你用「升维打击」的思路,那就是:
我能不能不刷题不内卷,就击败那些卷王
有这个思路,才是对的。
我们这本书,也就是为你「升维打击」奠基的。
黑桃5:构造法
构造法是转化/创新策略的一种常见方法。
中国建设时期,大庆油田的铁人王进喜说过一句话:「有条件要上,没有条件创造条件也要上」。
这句话就是构造法的精髓。
没有条件就创造条件。
本书中好几个案例,就涉及到了构造法。
例如泰勒斯测量金字塔高度,他构造了一个场景:在日照的时候(产生影子),自己走来走去,这样把自己当一条边,影子当一条边,构造一个和金字塔的相似三角形。甚至还可以选择自己的影子和身高相等的时候(构造出等腰三角形),避免比例转化,简化计算。
构造法的经典。
而黎曼发明黎曼几何,从他要解决的原始问题角度(二维曲面问题),也是一种构造,只是他构造了更大的问题和解决方案,进而以此为基础解决原始问题。
我们前面用「面积转化」解决鸡兔同笼,也是构造,构造了一个等价的图形问题,来解决鸡兔同笼问题。

在扑克中,构造法的守护神是刘徽。
刘徽是中国古代最伟大的数学家之一,他为经典数学著作《九章算术》所作的注,本身就是一部充满原创性思想的杰作。
其中,最能体现他「构造法」与「演化策略」完美结合的,莫过于他计算圆周率的「割圆术」。
在刘徽的时代,计算一个圆的周长和面积,是一个巨大的难题,因为圆是曲的,而当时所有的测量工具,都是直的。
面对这个曲直之争的难题,刘徽的思路,正是「没有条件,创造条件也要上」。他的核心思想是:
我虽然无法直接测量圆,但我可以构造一个与它极其相似、且我完全可以计算的多边形,用这个直的、可计算的图形,去无限逼近那个曲的、不可计算的圆。
接下来,刘徽做出了一个天才的、堪称「神级简化」的选择:他没有从正方形(四边形)或正三角形开始,而是选择了从「圆的内接正六边形」开始他的构造之旅。
为什么是正六边形?
因为在一个圆里,正六边形的边长,恰好就等于这个圆的半径!
这个选择,是一个极其优雅的「构造」。它让整个计算的初始条件,变得无比简单和明晰,完全避免了复杂的开方运算。
接下来,就是「演化」的登场。

刘徽想:
- 我已经有了6边形,不够精确。
- 我能否在6边形的基础上,构造出12边形?
- 在12边形的基础上,再构造出24边形?
- 再到48边形、96边形、192边形……
他通过一系列精妙的几何构造(添加辅助线、利用勾股定理),成功地找到了一个可以无限重复的「递归」算法,让他能够从n边形的边长,精确地计算出2n边形的边长。

他就这样,一步一步地,用更直的边,去「割」圆的弧,让多边形越来越接近圆。最终,他计算到了3072边形,得到了圆周率约等于3.1416的、在当时堪称世界之巅的精确结果。
刘徽的「割圆术」,是「构造法」的经典。当面对一个无法直接下手的难题时,高手会像一个棋手一样,主动地去「做棋」——构造一个极其有利的「初始局面」(正六边形),然后找到一个可以「演化」的制胜规则,最终将看似无法战胜的「神龙」(圆),分解为无数可以被轻松斩杀的「小蛇」(直角三角形)。
我们再来看这句话:「有条件要上,没有条件创造条件也要上」,这是强烈的进取心、创新精神,同时也是科学思想(没有条件要先创造条件)。
那么应试学习是什么呢?没有条件也要上,硬干。
蛮干精神。
违反科学原则。
所以失败是必然而长久的,成功是侥幸而短暂的。
黑桃4: 等价变形
等价变形是实现转化的基本手段。

这张牌的守护神,是韦达。
弗朗索瓦·韦达是16世纪的法国数学家,被誉为「符号代数之父」。他的贡献,可以说是为整个现代数学,提供了最基础的「操作系统」。
今天我们能够简洁快速的进行代数等价变形,也是他的贡献。
在韦达之前,代数学很大程度上是「文字代数」。解方程,就像在写一篇冗长的说明文。 比如,一个二次方程,可能会被当时的人描述成:「一个数,它的平方的三倍,加上它本身的四倍,等于五。求这个数。」
这种写法,不仅繁琐、低效,更致命的是,它让数学家无法对问题本身,进行灵活的、结构性的「变形」。
韦达的革命性贡献在于,他第一个系统性地、有意识地使用字母,来同时代表「未知数」(比如用元音字母 A, E, I, O, U)和「已知数」(比如用辅音字母 B, C, D)。
这个看似简单的改变,却是一次石破天惊的「升维打击」。它将代数,从具体的、一次性的「算术求解」,解放到了抽象的、普适的「符号游戏」之中。
正是因为有了这套符号系统,数学家们才第一次,可以像操纵「乐高积木」一样,对一个方程,进行各种纯粹形式上的「等价变形」,而不用去管它背后具体的数字和意义。
而「韦达定理」,正是这种「等价变形」思想的巅峰之作。
「韦达定理」的产物「二次求根公式」,核心是:
对于二次方程:$ax^2 + bx + c = 0 \quad (a \neq 0) $
其求根公式为: $ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $
这个定理的威力在于,它让我们可以「直接套用公式求解任何二次方程的根,彻底简化了二次方程求解」。
韦达,为我们提供了「变形」的工具(符号代数),又用他最著名的定理,展示了「变形」的威力。 他告诉我们,「等价变形」这把武器的精髓,就是:通过形式上的巧妙变化,达成实质上的惊人简化。
不仅要知道等价变形,更要知道为什么做等价变形
大多数同学遇到难题,就容易「没见过、没思路」。
做不出来正常,做出来也是碰运气。
然而高手,面对这种情况,还是会去探索寻找思路。
其实很多时候,问题反过来就是方向。
例如:「没见过」,那么你见过什么呢?
以二次求根公式为例。
大多数同学怎么学习这个知识点的呢?
老师讲二次求根公式是$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $ ,跟大家说这个公式很重要,是考点。
学渣同学们哗啦哗啦记笔记,把求根公式给抄一遍在笔记本上。
然后就开始做题,刷一啪啦的题目,就是套这个公式求解各种二次方程。
这就是直接从老师那里接收灌输拿到结论,然后开用。
学霸会跟着老师或者下来自己把求根公式推导一遍,基于配方法,然后得出结论,接下来就开始大量刷结论解方程。
这样其实还是局限在这个知识点的层次,局部的学习和理解知识。
而顶尖选手基于深度研究的思路,会不一样。
单纯从这个二次求根公式的角度,他们会有更深入的问题,会去研究思考原因。例如:
为什么要用配方法呢?怎么想到用配方法来求解二次方程的呢?
我们解题有一个基本原则:简化原则。就是把复杂的、未知的,简化为简单的、已知的。
这是我们的理科宪法第二条。

那么我们看二次方程$ax^2 + bx + c = 0 \quad (a \neq 0) $,这个在当时学习时是一个新问题。
我们没见过,不知道该怎么做。
这时候怎么办呢?尝试简化。
如何简化我们才会做呢?
二次方程不会解决,但是一次方程我们当时已经学过了,例如: $ax + b = 0 $这种通用一次方程,我们是会解决的。
那么,如果我们能把二次方程的求解问题,简化(转化)为一次方程的求解问题,不就能做了吗?
那么继续思考,具体怎么转化/简化呢?
暂时没有特别好的思路(你假设自己没看过答案)。
观察这个方程式$ax^2 + bx + c = 0 \quad (a \neq 0) $,我们一时想不到方法,那就尝试把这个方程式简化成更特殊形式看看。如果我们设b=0,也就是去掉bx项了,那就有 $ax^2 + c = 0 \quad (a \neq 0) $。
哎呀,这个我们能转化成一次方程吗?
可以,无非就是 $x^2 + \frac{c}{a} = 0 \quad (a \neq 0) $
移项之后变成 $x^2 = - \frac{c}{a} \quad (a \neq 0) $
这样就可以通过开方来把二次方程转化为一次方程拿到解了。
其实到这里,也就是有了一个最简单的二次方程形式:$x^2 = m $
对这种特殊形式的,没有一次项的二次方程,我们可以求解了。
那么接下来问题就是,如何能够把更普遍的二次方程$ax^2 + bx + c = 0 \quad (a \neq 0) $,转化为类似于 $x^2 = m $ 的形式呢?
把二次方程化为$x^2 + \frac{b}{a} x + \frac{c}{a} = 0 \quad (a \neq 0) $,基于前面的研究,我们核心是怎么把这个一次项给去掉。
这里就用了配方法,基于完全平方公式去掉了一次项,最终得到类似于$x^2 = m $ 的形式,产生了最终的结论,也就是二次求根公式。
这样,我们搞清楚了二次求根公式怎么来的。
学到了配方法。
了解了完全平方公式的一个相关应用,就是配方法。
了解了配方法的一个重要用途,那就是用来去掉二次式中的一次项,从而把二次式变成更简单的形式。
通过简化思维重新推导求解了二次根式。
而在知识体系推导演化角度,此前我们的知识点在一次方程以及求解公式,而现在基于简化思维,我们基于「一次方程求解」、「二次方程的代数表示」、「完全平方公式」这些前置知识点,围绕「二次方程求解」这个问题的推导,进一步演化产生了二次方程求根公式,以及相关的「配方法」。
这样知识体系也就拓展了。
作为新知识的「二次求根公式」,是这样在已有知识基础上逻辑推导出来的。
而且这个过程,还把诸如完全平方公式这样的知识点重新复习了一遍,加深了认识。
理解了这个逻辑,其实并不需要可以记忆。
忘记了再推一遍就很快了。
同时还把推导思路给复习了一遍。
而大多数同学则是记忆一个结论,不熟悉再次背诵一遍。
这个就完全不一样的逻辑了。
他们的结论,是搬过来套用的。
他们的知识推导过程,要么根本没做,要么就是简单的照着解一遍,没有真正思考为什么会这样去推导求解。
所以都是复制粘贴。
这样,一方面知识欠债,掌握不够深刻。
一方面智力欠债,因为缺乏研究分析深入推理。
还有解题思路方法也欠债了,因为哪怕是照着做了一遍,也没去思考「这个思路怎么出来的,为什么在这个步骤要这样求解」,这种背后的为什么,才是解决思维更灵活题目的关键。
很多同学看到比较考思维的题目,就无从下手,一看答案又觉得会做了,「一做就懵一讲就懂」。
一个原因,就是缺少这种日常去研究分析「这题为什么会这样做」的经验,去搞清楚问题的复杂性和简化策略,无脑搬运解法。
所以从这个案例,其实你真正把课本搞懂了,无论是基础知识,还是解题思路,都差不多了。
已经是一流水平。
黑桃三:反证法
反证法是一种非常巧妙的方法。
可以算是转化策略的一种应用。
但是这个转化,是先转化到目标的反面,但最后又转回来。
概要的说:
- 欲证其真,先证其伪
- 欲证其伪,先证其真
带有浓厚的辩证思维特点。
反证法的故事,也带有传奇色彩。
它有史记载的第一次登场,就引发了惊天危机。

而这个危机的源头,还要说到毕达哥拉斯定理的证明,以及毕达哥拉斯学派。
毕达哥拉斯诞生于靠近小亚细亚海岸的萨摩斯岛。在四处游学之后,他成立了一个兼具宗教、科学、哲学性质的帮派,也就是毕达哥拉斯学派。
这个学派有人员的限制,内部传授知识,并且对外保密。
毕达哥拉学派有一个基本信仰:万物皆数。他们相信数代表了真理,可以解释万物。
可能他们的信仰,更进一步。亚里斯多德说,毕达哥拉斯学派,把数看做真实物质世界的最终组成部分(类似于今天科学中的原子概念了)。
在那个时代,人们认识的数,是像1、2、3这种我们日常经验可以感知的数,也就是整数(严格的说正整数)。
所以毕达哥拉斯学派认为,任何事物,都可以表达为整数,或者整数的比。
数学证明引发的谋杀案
在证明了毕达哥拉斯定理之后,传说毕达哥拉斯学派欣喜若狂,杀了100头牛祭祀庆祝。
然而,好景不长。这个定理的证明,对于毕达哥拉斯学派而言,如同打开了潘多拉的魔盒。它释放出了一个幽灵。
这个幽灵是什么呢?
如果我们做一个直角边长为1的等腰直角三角形。
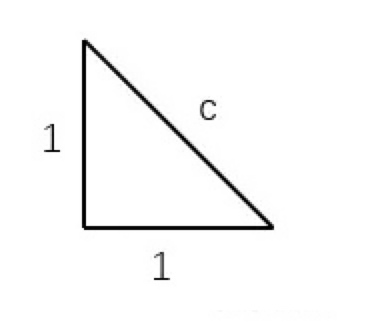 那么根据毕达哥拉斯定理,有 $ 1^2 + 1^2 = c^2 $
那么根据毕达哥拉斯定理,有 $ 1^2 + 1^2 = c^2 $
化简之后可得 $ c^2 = 2 $。
前面我们谈到,毕达哥拉斯学派信仰「万物皆数」。他们认为,任何事物,都可以表达为整数,或者整数的比。
首先,c不是一个整数(1之后的最小整数是2,而c大于1小于2)。
那么,按照毕达哥斯拉的理念,c应该可以表达为两个整数之比。
然而,在毕达哥拉斯学派中,有一个人叫做希帕索斯。他证明,这个c不能表达为整数之比。
他是如何证明的呢?
反证法的应用
希帕索斯使用了反证法。
他首先假设,c能够表达为两个整数之比,也就是假设c=p/q(这里p、q互质,否则还是可以化简得到一个互质的p、q形式)。
这样一来,(p/q)x(p/q)=2,化简之后得到pxp=2xqxp。
因为p和q互质,那么p、q最多只能有一个偶数(否则还可以继续化简)。
又因为pxp=2xqxq,也就是说pxp必然是偶数,那么p必然是偶数。
这样一来,q就必然是奇数。
既然q是奇数,等式的右边(2xqxq),一共就只有一个2的因子。
然而,在等式的左边,因为p是偶数,那么p至少有一个2的因子。pxp至少有两个2的因子。
这样一来,等式左边和右边不能相等。
因此,我们最开始的假设(c能够表达为两个整数之比)是错误的,c不能表达为两个整数之比。
这是一个非常漂亮的证明。希帕索斯使用的,是一些基本的整数和运算性质,例如奇偶性、整数的因数。反证法的应用很精彩。
有哲学思辨的美妙。
狂热的信仰
希帕索斯的证明非常漂亮,无懈可击。
然而这个证明,直接跟毕达哥拉斯学派的基本理念相冲突。
毕达哥拉斯学派信仰「万物皆数」。他们认为,数字代表了真理,任何事物,都可以表达为整数,或者整数的比。
今天,居然有了既不是整数,也不能表达为整数的比的长度。那么,「万物皆数」就站不住脚了。
从数学史的角度,这件事情称为第一次数学危机。
如果单纯从科学研究的观点,站不住脚是好事,证明理论研究有了新方向、新突破。承认问题,继续研究就行了呗。
但是如果从宗教信仰的角度,那就不一样了,「神」不灵了,世界崩溃了。
那怎么办呢?不能解决问题,但是可以解决提出问题的人啊。
于是希帕索斯被扔到海里喂鱼了。
可比数 vs 不可比数
尽管希帕索斯成了倒霉蛋,但他所发现的事实,依然存在。
这就导致了新的概念的产生,希腊人现在意识到,不是所有事物,都可以表达为两个整数之比的。
于是,希腊人有了「可比」(也翻译为「可公度」,和「不可比」(不可公度)的概念。
在希腊文中,希腊人用「λογος」,表示「可比之数」。而这个翻译到英文,比例的词根是ratio,可比之数也就翻译成了rational number,不可比之数则翻译成了irrational number。
从直观容易理解的角度,其实有理数更浅显的翻译,应该是「比数」。而无理数,则是「不可比数」或者「非比数」。例如 $ c ^ 2 = 2 $,这个c就是不可比的数。
从另外一方面,rational和irrational,本来也就是「理性」和「非理性」的意思。
毕达哥拉斯学派,学习数学是为了追求理性(虽然矛盾的他们又有对数的强烈的带有宗教性质的迷信色彩),他们认为数就代表了理性、能解释万物运作,所有事物都可以表达为整数和整数之比。
理解了在他们心目中,数与理性的关系,那么对有理数和无理数的概念,也就容易掌握。
儿子生爸爸
有个笑话说,妈妈问儿子,是爸爸大还是儿子大。
儿子说:一样大。
妈妈问为什么啊。
儿子说,因为生了我,爸爸才当爸爸的。
看上去是笑话,但背后却有一个道理。固然从生物体的角度,是现有爸爸这个人,再有儿子。
但从概念的角度,「爸爸」这个概念,却要从属于「儿子」这个概念。没有「儿子」,就没有「爸爸」。
如果脱离了「儿子」的概念,单纯讲「爸爸」,在现实生活中,我们一定觉得很荒谬。
但是在数学教课书里,这种逻辑上的脱节却是普遍的。用人教版初中数学教材为例,初一上引入「有理数」的概念,说「整数和分数统称有理数」。初一下又跳出无理数的概念。
然而从逻辑上,这两个概念是配套的。正因为发现了不可比的数,才需要一个「可比数」的概念来区分。否则就像希腊人之前那样,没有发现不可比的数,也就没必要叫「可比数」。本来数都是可比的,那还要这个概念干嘛。
教材把概念都搞得支离破碎,就难怪学生普遍缺乏对概念的理解了。
反过来,这也是为什么,你需要溯本求源,回到概念产生的原始现场。
这也是「爱智求真」,要探索概念的真相。

黑桃2: 倒推法
前面的反证法,是基于逆向思维的方法。
而倒推法,也是基于逆向思维。

倒推法的守护神,是帕普斯。
亚历山大的帕普斯,是生活在公元4世纪的、古希腊数学「黄金时代」最后一位伟大的几何学家。
他所处的时代,是一个创造力开始衰退,而更注重整理、注释和传承前人智慧的时代。帕普斯最伟大的著作《数学汇编》,就像一部「古希腊数学的百科全书」,为我们保存了大量已经失传的珍贵思想。
在这部巨著中,帕普斯做了一件极其重要、也极具开创性的事情:他第一次,系统性地、理论化地,为数学家们解决难题时的「思考过程」,进行了「立法」。
他将一个完整的解题过程,清晰地分为了两个方向完全相反的步骤:
第一步:「分析法」—— 这,就是「倒推法」的灵魂。
帕普斯这样定义它:
「我们假设问题已经被解决(所求已得),并顺着这个已解决的状态,一步步地逆向推导,看看它会引出哪些我们已知的、更简单的结论或前提。」
这就像一个侦探,拿到了最终的「犯罪现场」(已解决的状态),然后开始「时光倒流」,一步步地回溯,最终找到那个最初的「犯罪动机」(已知的前提)。
第二步:「综合法」 —— 也就是我们熟悉的正向推导。
帕普斯接着说,在我们通过「分析法」找到了那条从「终点」到「起点」的秘密路径之后,我们就可以反过来,从那个「已知的起点」出发,沿着刚才找到的路径,一步步地正向构建出我们的证明,最终充满信心地抵达那个「未知的终点」。
帕普斯的伟大之处在于,他将数学家们头脑中那些「不可言说」的、模糊的「逆向思考」直觉,第一次用清晰的语言,数理成了一套「标准作业流程」。
他告诉我们,「倒推」,不是一种碰运气的「奇技淫巧」,而是一种与「正向思维」同样重要、甚至在「探索未知」时更为根本的科学方法。当你正向的路走不通时,不妨试试,从终点出发,倒着走回来。
综合运用顺推和倒推,是求知和解题的基本能力。
总结:策略武器与谋略能力
总结一下我们的黑桃(策略武器),黑桃牌可以分为3个层次:
第一层:最高统帅
- ♠️A: 简化的5大策略
它提出了「化繁为简」的五条核心战略路径,是所有策略的总纲。
第二层:五大核心战略
- ♠️K: 演化策略
- ♠️Q: 形象策略
- ♠️J: 抽象策略
- ♠️10: 转化策略
- ♠️9: 创新策略
这五张牌,是我们为「化繁为简」这个宪法第二条,配备的五支「主力军团」。
第三层:具体的战术武器
- ♠️8: 数形结合
- ♠️7: 分而治之
- ♠️6: 升维打击
- ♠️5: 构造法
- ♠️4: 等价变形
- ♠️3: 反证法
- ♠️2: 倒推法
这些牌,则是更具体的、在不同战场上落实五大战略的「特种兵器」。
从能力角度,黑桃代表谋略能力。
很多同学看到问题就「束手无策」,「策」就是策略,这就是谋略能力的低下。
掌握这些策略武器,在前面「现象武器」(红桃)和「线索武器」(方块)的支持下,会让你成为真正的谋略高手。
从另外一个层面,我们讲一个人「足智多谋」(羽扇纶巾诸葛亮)。黑桃策略牌主要关注「多谋」,而即将登场的梅花哲思牌,则更关注底层的「足智」。
这两者,相辅相成。